Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

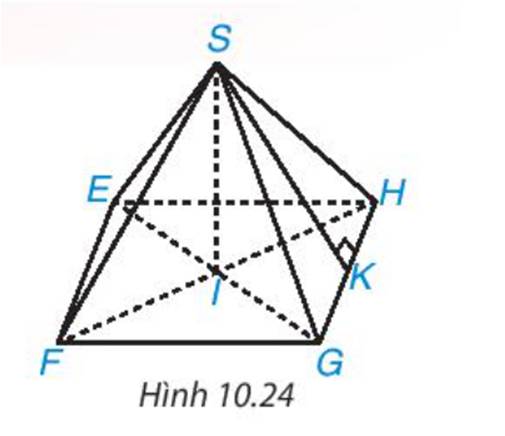
- Đỉnh: S
- Cạnh bên: SE, SF, SG, SH
- Mặt bên: SEF, SFG, SGH. SEH
- Mặt đáy: EFGH
- Đường cao: SI
- Một trung đoạn: SK

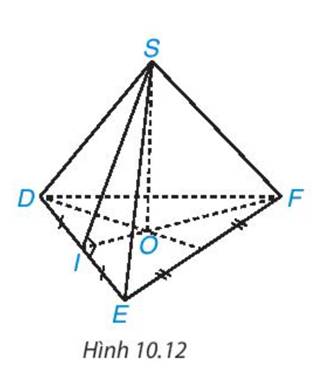
- Đỉnh: S
- Cạnh bên: SD, SE, SF
- Mặt bên: SDE, SEF, SDF
- Mặt đáy: DEF
- Đường cao: SO
- Một trung đoạn: SI

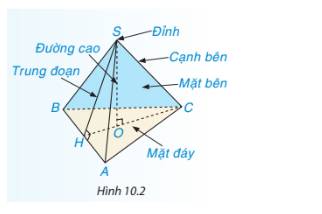
Hình chóp tam giác đều S. ABC có:
- Đỉnh: S
- Cạnh bên: SA, SB, SC.
- Mặt đáy: tam giác ABC.
- Đường cao: SO.
- Trung đoạn: SH

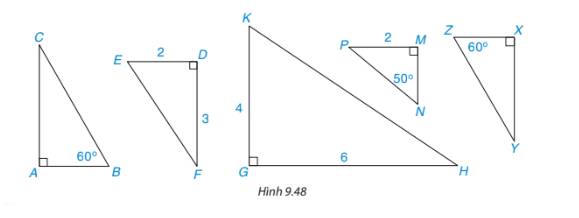
Các cặp tam giác vuông đồng dạng:
\(\begin{array}{l}\Delta ABC \backsim \Delta X{\rm{Z}}Y(\widehat A = \widehat X;\widehat B = \widehat Z)\\\Delta E{\rm{D}}F \backsim \Delta KGH\left( {\frac{{E{\rm{D}}}}{{KG}} = \frac{{DF}}{{GF}};\widehat {E{\rm{D}}F} = \widehat {KGH}} \right)\end{array}\)

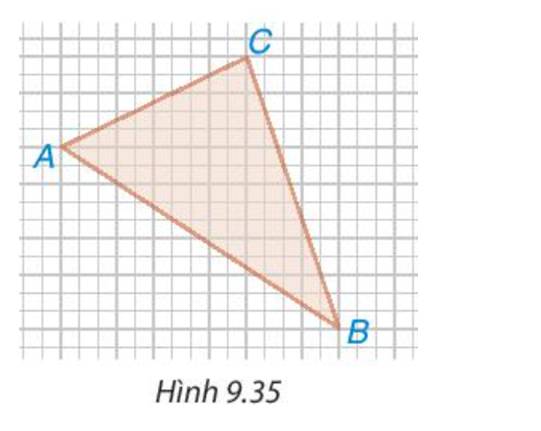
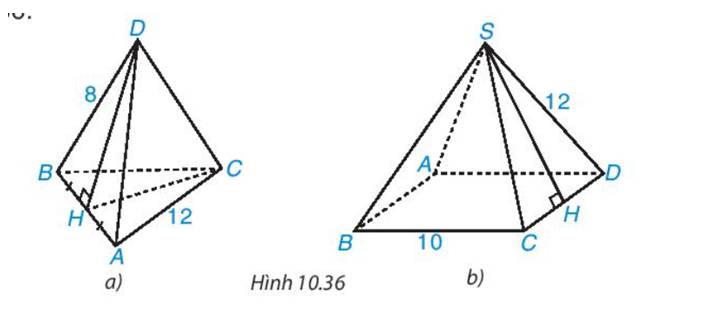
\(AC^2=100+25=125\Rightarrow AC=5\sqrt[]{5}\left(cm\right)\)
\(AB^2=100+225=325\Rightarrow AB=5\sqrt[]{13}\left(cm\right)\)
\(BC^2=225+25=250\Rightarrow BC=5\sqrt[]{10}\left(cm\right)\)

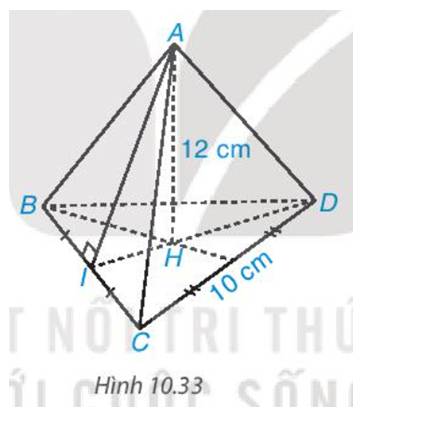
- Xét tam giác BID vuông tại I, có
\(I{{\rm{D}}^2} = B{{\rm{D}}^2} - B{I^2} = {10^2} - {5^2}\)
=> ID ≈ 8,66 (cm)
- Diện tích tam giác BCD là:
\({S_{BC{\rm{D}}}} = \frac{1}{2}.I{\rm{D}}.BC = \frac{1}{2}.8,66.10 = 43,3\left( {c{m^2}} \right)\)
- Thể tích hình chóp là:
\(V = \frac{1}{3}.S.h = \frac{1}{3}.43,3.12 \approx 173,2(c{m^3})\)

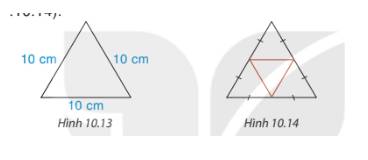
* Nửa chu vi của tam giác ABC là:
\(\left( {12 + 12 + 12} \right):2 = 18(m)\)
Xét tam giác HBD vuông tại H, có:
\(\begin{array}{l}H{{\rm{D}}^2} = B{{\rm{D}}^2} - B{H^2} = {8^2} - {6^2}\\ \Rightarrow H{\rm{D}} = 2\sqrt 7 \end{array}\)
Diện tích xung quanh của hình chóp tam giác đều là:
\({S_{xq}} = p.d = 18.2\sqrt 7 = 36\sqrt 7 \left( {{m^2}} \right)\)
* Nủa chu vi của tứ giác ABCD là:
\(\left( {10.4} \right):2 = 20\)
Xét tam giác SHD vuông tại H, ta có:
\(\begin{array}{l}S{H^2} = S{{\rm{D}}^2} - H{{\rm{D}}^2} = {12^2} - {6^2} = 119\\ \Rightarrow SH = \sqrt {119} \end{array}\)
Diện tích xung quanh của hình chóp tứ giác đều là:
\({S_{xq}} = p.d = 20.\sqrt {119} = 20\sqrt {119} \left( {{m^2}} \right)\)

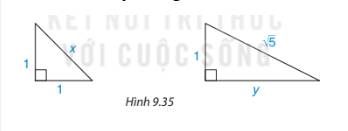
\(x^2=1^2+1^2\left(pythagore\right)\\ \Rightarrow x=\sqrt{2}\\ \sqrt{5}^2=1^2+y^2\left(pythagore\right)\\ \Rightarrow y=\sqrt{4}=2\)
a) \(x^2=1^2+1^2=2\Rightarrow x=\sqrt[]{2}\)
b) \(\left(\sqrt[]{5}\right)^2=y^2+1^2\Rightarrow y^2=5-1=4\Rightarrow y=2\)
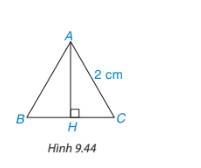
Vì tam giác ABC là tam giác đều, \(AH \bot BC\) nên H là trung điểm của BC suy ra
\(HB = HC = \frac{{BC}}{2} = \frac{2}{2} = 1\)(cm)
Áp đụng định lí Pythagore trong tam giác AHC ta có:
\(\begin{array}{l}A{C^2} = A{H^2} + H{C^2} \Rightarrow A{H^2} = A{C^2} - H{C^2} = {2^2} - {1^2} = 3\\ \Rightarrow AH = \sqrt 3 \approx 1,73(cm)\end{array}\)
Vậy chiều cao của tam giác đều là 1,73cm.