S
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
PT
26 tháng 4 2017
a) Ta có:
3A= \(1+\dfrac{1}{3}+\dfrac{1}{3^2}+\dfrac{1}{3^3}+...+\dfrac{1}{3^{99}}\left(1\right)\)
A= \(\dfrac{1}{3}+\dfrac{1}{3^2}+\dfrac{1}{3^3}+...+\dfrac{1}{3^{100}}\left(2\right)\)
Lấy (1) - (2) ta được:
1-\(\dfrac{1}{3^{100}}\)
b) Ta xét:
\(\dfrac{1}{1.2}-\dfrac{1}{2.3}=\dfrac{2}{1.2.3},...,\dfrac{1}{37.38}-\dfrac{1}{38.39}=\dfrac{2}{37.38.39}\)
Ta có:
2B=\(\dfrac{2}{1.2.3}+\dfrac{2}{2.3.4}+..+\dfrac{2}{37.38.39}\)
=\(\left(\dfrac{1}{1.2}-\dfrac{1}{2.3}\right)+\left(\dfrac{1}{2.3}-\dfrac{1}{3.4}\right)+..+\left(\dfrac{1}{37.38}-\dfrac{1}{38.39}\right)\)
=\(\dfrac{1}{1.2}-\dfrac{1}{38.39}=\dfrac{740}{38.39}=\dfrac{370}{741}\)
Vậy \(\dfrac{2}{1.2.3}+\dfrac{2}{2.3.4}+\dfrac{2}{3.4.5}+..+\dfrac{2}{37.38.39}\)
=\(\dfrac{370}{741}\)
Nếu bn cảm thấy mk đúng tick cho mk nhé!
AN
1 tháng 9 2017
A= \(\dfrac{1}{1.2.3}+\dfrac{1}{2.3.4}+\dfrac{1}{4.5.6}+....+\dfrac{1}{37.38.39}\)
A=\(\dfrac{1}{1}-\dfrac{1}{39}\)
A=\(\dfrac{38}{39}\)
còn lại tự làm do mình có việc chút
CD
4
4 tháng 5 2017
Câu hỏi của Dung Van - Toán lớp 6 | Học trực tuyến tìm kĩ trước khi hỏi nhé.
K
20 tháng 3 2018
Ta có :
\(\dfrac{1}{1.2}-\dfrac{1}{2.3}=\dfrac{3}{1.2.3}-\dfrac{1}{1.2.3}=\dfrac{2}{1.2.3}\)
\(\dfrac{1}{2.3}-\dfrac{1}{3.4}=\dfrac{4}{2.3.4}-\dfrac{2}{2.3.4}=\dfrac{2}{2.3.4}\)
...
Do đó :
\(\dfrac{1}{1.2.3}=\dfrac{1}{2}\left(\dfrac{1}{1.2}-\dfrac{1}{2.3}\right)\)
\(\dfrac{1}{2.3.4}=\dfrac{1}{2}\left(\dfrac{1}{2.3}-\dfrac{1}{3.4}\right)\)
Vậy :
\(M=\dfrac{1}{2}\left(\dfrac{1}{1.2}-\dfrac{1}{2.3}+\dfrac{1}{2.3}-\dfrac{1}{3.4}+\dfrac{1}{3.4}-\dfrac{1}{4.5}+...+\dfrac{1}{10.11}-\dfrac{1}{11.12}\right)\)
\(=\dfrac{1}{2}\left(\dfrac{1}{1.2}-\dfrac{1}{11.12}\right)\)
\(=\dfrac{1}{2}\left(\dfrac{1}{2}-\dfrac{1}{132}\right)\)
\(=\dfrac{1}{2}.\dfrac{65}{132}=\dfrac{65}{264}\)
22 tháng 3 2017
\(\dfrac{1}{2}\left(\dfrac{1}{1.2}+\dfrac{1}{2.3}+...+\dfrac{1}{18.19}+\dfrac{1}{19.20}\right)\) Gio thi tu ma lam ko thích viết nữa mệt
23 tháng 3 2017
bn ơi mk nghĩ bn nên tôn trọng mk một chút! Nếu bn giúp đc thì mk cảm ơn rất nhiều. Còn bn không làm đc thì để cho người khác làm! bn ko thích làm thì mk cx ko mong bn giải nửa chừng như vậy, mk vừa ko hiểu j mà còn bị tự ái khi bn nói như vậy, mong bn hiểu!!mk góp ý thật lòng, ko chỉ đối với mk mà với những bn khác cx zậy!!
LT
1
17 tháng 4 2017
Ta có :
\(S=\dfrac{1}{1.2.3}+\dfrac{1}{2.3.4}+..............+\dfrac{1}{98.99.100}\)
\(S=\dfrac{1}{2}\left(\dfrac{2}{1.2.3}+\dfrac{2}{2.3.4}+................+\dfrac{2}{98.99.100}\right)\)
\(S=\dfrac{1}{2}\left(\dfrac{1}{1.2}-\dfrac{1}{2.3}+\dfrac{1}{2.3}-\dfrac{1}{3.4}+...........+\dfrac{1}{98.99}-\dfrac{1}{99.100}\right)\)
\(S=\dfrac{1}{2}\left(\dfrac{1}{1.2}-\dfrac{1}{99.100}\right)\)
\(S=\dfrac{1}{2}\left(\dfrac{1}{2}-\dfrac{1}{9900}\right)\)
\(S=\dfrac{1}{2}.\dfrac{4949}{9900}\)
\(S=\dfrac{4949}{19800}\)
~ Chúc bn học tốt ~
NM
3
21 tháng 3 2017
E=\(\dfrac{1}{1.2.3}+\dfrac{1}{2.3.4}+...+\dfrac{1}{98.99.100}\)
* Áp dụng công thức: \(\dfrac{k}{n.\left(n+k\right)}\)=\(\dfrac{1}{n}-\dfrac{1}{n+k}\)
ta có : \(\dfrac{1}{1.2}-\dfrac{1}{2.3}+\dfrac{1}{2.3}-\dfrac{1}{3.4}+\dfrac{1}{3.4}-....+\dfrac{1}{98.99}-\dfrac{1}{99.100}\)
E=\(\dfrac{1}{1.2}-\dfrac{1}{99.100}\)
E= ........(tính ra)
NT
1
14 tháng 4 2017
\(\dfrac{1}{1.2.3}+\dfrac{1}{2.3.4}+...+\dfrac{1}{10.11.12}\)
\(=\dfrac{1}{2}\left(\dfrac{2}{1.2.3}+\dfrac{2}{2.3.4}+...+\dfrac{2}{10.11.12}\right)\)
\(=\dfrac{1}{2}.\left(\dfrac{1}{1.2}-\dfrac{1}{2.3}+\dfrac{1}{2.3}-\dfrac{1}{3.4}+...+\dfrac{1}{10.11}-\dfrac{1}{11.12}\right)\)
\(=\dfrac{1}{2}.\left(\dfrac{1}{1.2}-\dfrac{1}{11.12}\right)\)
\(=\dfrac{1}{2}.\left(\dfrac{1}{2}-\dfrac{1}{132}\right)\)
\(=\dfrac{1}{2}.\dfrac{65}{132}\)
\(=\dfrac{65}{264}\)
Vậy...
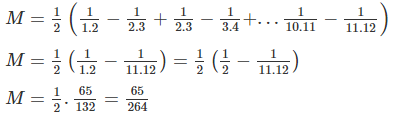
\(A=\dfrac{1}{1.2.3}+\dfrac{1}{2.3.4}+...+\dfrac{1}{37.38.39}\)
\(A=\dfrac{1}{2}\left(\dfrac{2}{1.2.3}+\dfrac{2}{2.3.4}+...+\dfrac{2}{37.38.39}\right)\)
\(A=\dfrac{1}{2}\left(\dfrac{1}{1.2}-\dfrac{1}{2.3}+\dfrac{1}{2.3}-\dfrac{1}{3.4}+...+\dfrac{1}{37.38}-\dfrac{1}{38.39}\right)\)
\(A=\dfrac{1}{2}\left(\dfrac{1}{1.2}-\dfrac{1}{38.39}\right)\)
\(A=\dfrac{1}{2}.\left(\dfrac{1}{2}-\dfrac{1}{1482}\right)\)
\(A=\dfrac{1}{2}.\dfrac{370}{741}=\dfrac{185}{741}\)