K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
KB
20 tháng 10 2018
a,Ta có: x- 1/2= y- 2/3⇒ y= x- 1/2 +2/3= x+ 1/6
x- 1/2= z- 3/4⇒ z= x+ 1/4
⇒ x- 2y+3z= 24
⇔ x- 2( x+ 1/6)+ 3( x+1/4)= 24
⇔ x- 2x- 1/3+ 3x+ 3/4= 24
⇔ 2x= 283/12
⇔ x= 283/24
b, Ta có: xy= -30⇒ x= -30/y
yz= 42⇒ z= 42/y
lại có: z- x= -12
⇒ 42/y+ 30/y= -12
⇔ 72/y= -12
⇒ y= -6
⇒ x= 5; z= -7
26 tháng 9 2016
Sao tự nhiên thấy đắng lòng quá, e cx đang định hỏi bài nỳ. Nghĩ hoài hổng ra. haizz... 
Q
29 tháng 12 2017
*Làm tắt
\(\dfrac{x}{5}=\dfrac{y}{3}=\dfrac{z}{2};x+2y+3z=34\Rightarrow\dfrac{x}{5}=\dfrac{2y}{6}=\dfrac{3z}{6}\Rightarrow\dfrac{x+2y+3z}{5+6+6}=\dfrac{34}{17}=2\)
\(\dfrac{x}{5}=2\Rightarrow x=10;\dfrac{y}{3}=2\Rightarrow y=6;\dfrac{z}{2}=4\Rightarrow z=4\)
NT
29 tháng 12 2017
\(\dfrac{x}{5}=\dfrac{y}{3}=\dfrac{z}{2}=\dfrac{x+2y+3z}{5+6+6}=\dfrac{34}{17}=2\\ \Rightarrow x=10;y=6;z=4\)
AP
1
NV
Nguyễn Việt Lâm
Giáo viên
30 tháng 9 2019
Biến đổi tương đương:
\(3x^2+3y^2+3z^2\ge x^2+y^2+z^2+2xy+2yz+2zx\)
\(\Leftrightarrow2x^2+2y^2+2z^2-2xy-2yz-2zx\ge0\)
\(\Leftrightarrow\left(x-y\right)^2+\left(y-z\right)^2+\left(z-x\right)^2\ge0\) (luôn đúng)
Dấu "=" xảy ra khi \(x=y=z\)
HT
2
DH
6 tháng 7 2017
Sửa đề:
Chứng minh rằng:
\(8x+8y+8z\le4^{x+1}+4^{y+1}+4^{y+2}\)
Ta có:
\(8x+8y+8z=8.\left(x+y+z\right)=8.6=48\)(1)
Áp dụng bất đẳng thức AM-GM ta có:
\(4^{x+1}+4^{y+1}+4^{z+1}\ge3\sqrt[3]{4^{x+1}.4^{y+1}.4^{z+1}}\)
\(\Rightarrow4^{x+1}+4^{y+1}+4^{z+1}\ge3\sqrt[3]{4^{x+y+z+3}}\)
\(\Rightarrow4^{x+1}+4^{y+1}+4^{z+1}\ge3\sqrt[3]{4^{6+3}}\)
\(\Rightarrow4^{x+1}+4^{y+1}+4^{z+1}\ge3\sqrt[3]{4^9}\)
\(\Rightarrow4^{x+1}+4^{y+1}+4^{z+1}\ge3.64\)
\(\Rightarrow4^{x+1}+4^{y+1}+4^{z+1}\ge192\)(2)
Dấu "=" sảy ra khi \(x=y=z=2\).
Từ (1) và (2) suy ra:
\(8x+8y+8z\le4^{x+1}+4^{y+1}+4^{y+2}\)(đpcm)
Chúc bạn học tốt!!!
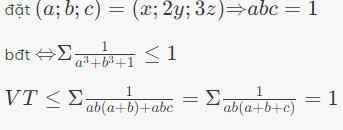
\(5x=8y=20z\Rightarrow\dfrac{x}{160}=\dfrac{y}{100}=\dfrac{z}{40}=\dfrac{x-y-z}{160-100-40}=\dfrac{3}{20}\)
\(\Rightarrow\left\{{}\begin{matrix}x=24\\y=15\\z=6\end{matrix}\right.\)
Lần sau đăng ở mục Toán 7 nha bạn :)
\(5x=8y=20z\Leftrightarrow\left\{{}\begin{matrix}5x=8y\\8y=20z\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{x}{8}=\dfrac{y}{5}\\\dfrac{y}{20}=\dfrac{z}{8}\end{matrix}\right.\Leftrightarrow\dfrac{x}{32}=\dfrac{y}{20}=\dfrac{z}{8}\)
Áp dụng tính chất dãy tỉ số bằng nhau:
\(\dfrac{x}{32}=\dfrac{y}{20}=\dfrac{z}{8}=\dfrac{x-y-z}{32-20-8}=\dfrac{3}{4}\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{3}{4}.32=24\\y=\dfrac{3}{4}.20=15\\z=\dfrac{3}{4}.8=6\end{matrix}\right.\)
Vậy ...