
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đặt \(\frac{x}{2}=\frac{y}{5}=k\Rightarrow x=2k;y=5k\)
thay x=2k;y=5k vào xy=10 ta được:
5k.2k=10
10k2=10
k2=1
=>k=1 hoặc k=-1
Với k=1 thì : x=5.1=5;y=2.1=2
Với k=-1 thì: x=5.(-1)=-5 ; y=2.(-1)=-2
\(\frac{x}{2}=\frac{y}{5}=>\frac{x}{2}.\frac{y}{5}=\frac{y}{5}.\frac{y}{5}=>\frac{xy}{10}=\frac{y^2}{25}=>\frac{10}{10}=\frac{y^2}{25}=>1=\frac{y^2}{25}=>y^2=25=5^2\)
=>y=5


Giải:
Đặt \(\frac{x}{2}=\frac{y}{5}=k\)
\(\Rightarrow x=2k,y=5k\)
Ta có: \(xy=10\)
\(\Rightarrow2k5k=10\)
\(\Rightarrow10k^2=10\)
\(\Rightarrow k^2=1\)
\(\Rightarrow k=\pm1\)
+) \(k=1\Rightarrow x=2;y=5\)
+) \(k=-1\Rightarrow x=-2;y=-5\)
Vậy cặp số \(\left(x;y\right)\) là \(\left(2;5\right);\left(-2;-5\right)\)

Theo bài ra ta có:
x/2=y/5
=>x=2y/5
Vậy ta có:
xy=10
2y/5.y=10
2y2/5=10
2y2=50
y2=25
y=5 hoặc y=-5
y=5 =>x=2
y=-5 =>x=-2
tìm x và y biết :
x/2 =y/5 và x.y=10
\(\frac{x}{2}=\frac{y}{5}\)
THeo tính chất của dãy tỉ số bằng nhau ta có :
\(\frac{x}{2}=\frac{y}{5}=\frac{xy}{2.5}=\frac{10}{10}=1\)
\(\frac{x}{2}=1\Rightarrow x=1.2=2\)
\(\frac{y}{5}=1\Rightarrow y=1.5=5\)
knha

đặt \(\frac{x}{2}=\frac{y}{5}=k\)
\(\Rightarrow x=2k;y=5k\)
Mà xy = 10
\(\Rightarrow\)\(2k.5k=10\)
\(\Rightarrow10k^2=10\)
\(k^2=10:10\)
\(k^2=1\)
\(\Rightarrow\orbr{\begin{cases}k=1\\k=-1\end{cases}}\)
Nếu k = 1 thì x = 2 ; y = 5
Nếu k = -1 thì x = -2 ; y = -5
Vậy ...
ADTC dãy tỉ số bằng nhau
Ta có :
\(\frac{x}{2}=\frac{y}{5}=\frac{x.y}{2.5}=\frac{10}{10}=1\)
\(.\frac{x}{2}=1\Leftrightarrow x=2\)
\(.\frac{y}{5}=1\Leftrightarrow y=5\)
\(\Rightarrow\hept{\begin{cases}x=2\\y=5\end{cases}}\)

Áp dụng tính chất của dãy tỉ số bằng nhau ta có:
\(\frac{x}{2}=\frac{y}{5}=k\)
\(\Rightarrow x=2k\)
\(\Rightarrow y=5k\)
\(\Rightarrow x.y=2k.5k=10k^2\)
\(\Rightarrow k^2=1\Rightarrow\hept{\begin{cases}k=1\\k=-1\end{cases}}\)
Với \(k=1\Rightarrow x=2.1=2\Rightarrow y=5.1=5\)
Với \(k=-1\Rightarrow x=-1.2=-2\Rightarrow y=-1.5=-5\)
đặt \(\frac{x}{2}=\frac{y}{5}=k\Rightarrow x=2k\)và y=5k mà x\(\times\)y=10\(\Rightarrow2k\times5k=10\)\(\Leftrightarrow10k^2=10\)
\(\Rightarrow k^2=10:10\Rightarrow k^2=1\)
tiếp theo là ...........................................

đặt x/2=y/5=k
=>x=2k;y=5k
theo đề :
x.y=10
=>2k.5k=10
10k2=10
k2=1
k=-1 hoặc 1
với k=1 thì x=2.k=2.1=2
y=5.k=5.1=5
với k=-1 thì x=2.k=2.(-1)=-2
y=5.k=5.(-1)=-5
vậy x=2;y=5 hoặc x=-2;y=-5

Ta có: \(\frac{x}{2}=\frac{y}{5}\)=> \(\frac{x^2}{2}=\frac{xy}{5}=\frac{10}{5}=2\)
=> x2 = 2.2 = 4
=> x = 2 hoặc x = -2
+) Nếu x = 2 => y = 10:2 = 5
+) Nếu x = -2 => y = 10:(-2) = -5
Vậy: (x;y)\(\in\){(2;5);(-2;-5)}
\(\frac{x}{2}=\frac{y}{5}\Rightarrow\frac{x.x}{2.2}=\frac{x.y}{2.5}\Rightarrow\frac{x^2}{4}=\frac{10}{10}=1\Rightarrow x^2=4\Rightarrow x^2=2^2\Rightarrow x\in\left\{2;-2\right\}\)
\(\frac{2}{2}=\frac{y}{5}\Rightarrow1=\frac{y}{5}\Rightarrow y\in\left\{5;-5\right\}\)
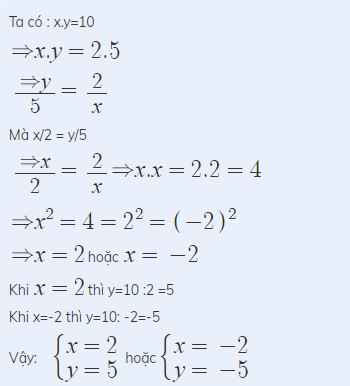
đặt \(\frac{x}{2}=\frac{y}{5}=k\Rightarrow x=2k;y=5k\)
thay x=2k ; y=5k vào x.y=10 ta được:
2k.5k=10
10 .k2=10
k2=1
=>k=1 hoặc k=-1
với k=1 thì
x=2.1=2
y=5.1=5
với k=-1 thì
x=2.(-1)=-2
y=5.(-1)=-5
Ta có : x.y=10
\(\Rightarrow x.y=2.5\)
\(\frac{\Rightarrow y}{5}=\frac{2}{x}\)
Mà x/2 = y/5
\(\frac{\Rightarrow x}{2}=\frac{2}{x}\)\(\Rightarrow x.x=2.2=4\)
\(\Rightarrow x^2=4=2^2=\left(-2\right)^2\)
\(\Rightarrow x=2\)hoặc \(x=-2\)
Khi \(x=2\)thì y=10 :2 =5
Khi x=-2 thì y=10: -2=-5
Vậy: \(\hept{\begin{cases}x=2\\y=5\end{cases}}\)hoặc\(\hept{\begin{cases}x=-2\\y=-5\end{cases}}\)
Cảm ơn các bạn vì đã xem câu trả lời của mìnk . Tuy nó hơi dài nhưng chắc cũng dễ hiểu !!!!!!!