Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Thử `p=2`
`=>p+2=4(HS)`
`=>p=2`(loại).
Thử `p=3`
`=>p+12=15(HS)`
`=>p=3`(loại).
Thử `p=5`
`=>` \begin{cases}p+2=7(SNT)\\p+6=11(SNT)\\p+8=13(SNT)\\p+12=17(SNT)\\p+14=19(SNT)\\\end{cases}
`=>p=5(TM)`
Nếu `p>5` mà p là SNT
`=>p cancel{vdost} 5`
`=>p=5k+1,5k+2,5k+3,5k+4`
`+)p=5k+1=>p+14=5k+15 vdots 5`
`=>p=5k+1` (loại).
`+)p=5k+2=>p+8=5k+10 vdots 5`
`=>p=5k+2` (loại).
`+)p=5k+3=>p+12=5k+15 vdots 5`
`=>p=5k+3` (loại).
`+)p=5k+4=>p+6=5k+10 vdots 5`
`=>p=5k+4` (loại).
Vậy `p=5`

Mình Nghĩ Câu Này Cũng Dễ Chứ Đâu Khó Đâu
Mình Không Cố í xúc phạm đâu
Câu này là p = 5
Câu Này Dễ Nên Mình Không Giải Chi Tiết Nha Bạn

Lời giải:
Xét số dư của $p$ khi chia cho $5$
Nếu $p=5k(k\in\mathbb{N}$ thì $p\vdots 5$. Mà $p$ là số nguyên tố nên $p=5$. Thay vào thấy các số đã cho đều là nguyên tố (thỏa mãn)
Nếu $p=5k+1(k\in\mathbb{N}\Rightarrow p+14=5k+15\vdots 5$. Mà $p+14>5$ nên không thể là số nguyên tố (loại)
Nếu $p=5k+2(k\in\mathbb{N}\Rightarrow p+8=15k+10\vdots 5$. Mà $p+8>5$ nên không thể là số nguyên tố (loại)
Nếu $p=5k+3(k\in\mathbb{N}\Rightarrow p+12=5k+15\vdots 5$. Mà $p+12>5$ nên không thể là số nguyên tố (loại)
Nếu $p=5k+4(k\in\mathbb{N}\Rightarrow p+6=5k+10\vdots 5$. mà $p+6>5$ nên không thể là số nguyên tố (loại)
Vậy $p=5$


Câu b:

Đến đoạn này cũng xét như câu a
Câu c:
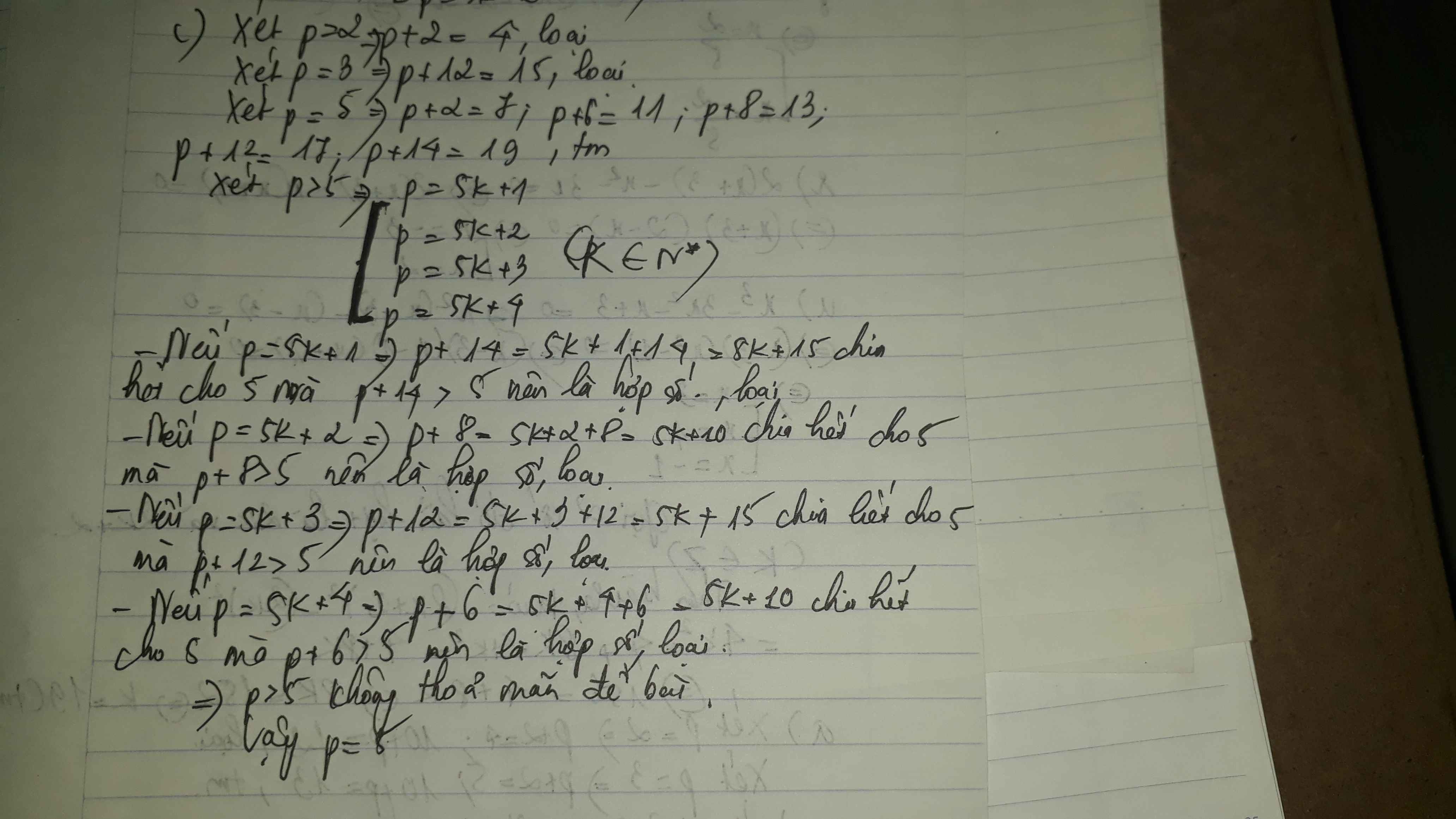


p + 12 , k phải p +22
p+12 chứ, lúc ấy p=5 nha