Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Sửa đề: Diện tích hình chữ nhật đó giảm đi 6m vuông
Gọi chiều dài, chiều rộng lần lượt là a,b
Nửa chu vi hình chữ nhật là 38/2=19
=>a+b=19
Theo đề, ta có hệ phương trình:
a+b=19 và (a+2)(b-1)=ab-19
=>a+b=19 và -a+2b=-17
=>a=55/3 và b=2/3


a: \(S=\left(30-x\right)\left(40-x\right)\)
\(=\left(x-30\right)\left(x-40\right)=x^2-70x+1200\)
=>S không là hàm số bậc nhất đối với x
\(P=2\left[30-x+40-x\right]=2\left(70-2x\right)=-4x+140\)
=>P là hàm số bậc nhất đối với x
b: Khi x=0 thì \(P=-4\cdot0+140=140\)
Khi x=1 thì \(P=140-4=136\)
Khi x=2 thì \(P=140-8=132\)
Khi x=3 thì \(P=140-12=128\)
Khi x=4 thì P=140-4*4=124

Lời giải:
Gọi chiều dài và chiều rộng của hình chữ nhật là $a,b$ (m)
Theo bài ra ta có:
$a+b=134:2=67$
$(a-1)(b-1)=28^2=784$
$\Leftrightarrow ab-(a+b)+1=784$
$\Leftrightarrow ab-67+1=784$
$\Leftrightarrow ab=850$
Từ $a+b=67$ và $ab=850$ áp dụng định lý Viet đảo thì:
$a,b$ là nghiệm của pt:
$X^2-67X+850=0$
$\Rightarrow (a,b) = (50,17)$
Mà $a>b$ nên chiều dài là 50 m, chiều rộng là 17m

Sau khi tăng kích thước của mỗi chiều, ta được hình chữ nhật A’B’C’D’ có chiều dài A’B’ = (40 + x) cm, chiều rộng B’C’ = (25 + x) cm.
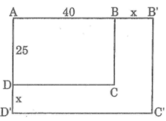
Diện tích hình chữ nhật mới:
S = (40 + x)(25 + x) = 1000 + 65x + x 2
S không phải là hàm số bậc nhất đối với x vì có bậc của biến số x là bậc hai.
Chu vi hình chữ nhật mới:
P = 2.[(40 + x) + (25 + x)] = 4x + 130
P là hàm số bậc nhất đối với x có hệ số a = 4, hệ số b = 130.

Nửa cv khu đất hcn là 48:2=24(m)
Chiều dài khu đất hcn là \(24:\left(2+1\right)\cdot2=16\left(m\right)\)
Chiều rộng khu đất hcn là \(24-16=8\left(m\right)\)
Diện tích khu đất hcn là \(8\cdot16=128\left(m^2\right)\)
Cạnh khu đất hv là \(\sqrt{128}\approx11,3\left(m\right)\)

Gọi chiều dài và chiều rộng của sân bóng lần lượt là \(x,y\left(m\right);x,y>0\).
Vì chu vi là \(140m\)nên \(2\left(x+y\right)=140\Leftrightarrow x+y=70\)
Vì giảm chiều rộng đi \(5m\)tăng chiều dài thêm \(8m\)thì diện tích sân bóng không đổi nên
\(\left(x+8\right)\left(y-5\right)=xy\Leftrightarrow-5x+8y=40\)
Ta có hệ phương trình:
\(\hept{\begin{cases}x+y=70\\-5x+8y=40\end{cases}}\Leftrightarrow\hept{\begin{cases}5x+5y=350\\-5x+8y=40\end{cases}}\Leftrightarrow\hept{\begin{cases}x=40\\y=30\end{cases}}\)(thỏa mãn)
Vậy chiều dài là \(40m\)chiều rộng là \(30m\).

Gọi kích thước của hcn đó là a và b (cm; a,b > 0 )
Ta có : nửa chu vi của hcn đó là:
a+b = \(\frac{34}{2}\) =17 (1)
Mà : đường chéo của hcn = 13cm
=> \(\sqrt{a^2+b^2}=13\) (2)
=> cặp số thỏa mãn (1) và (2) là 12 và 5
Hay chiều dài của hcn là 12 cm
chiều rộng của hcn là 5 cm
Gọi chiều dài là a, chiều rộng là b
Ta có :
\(a.b=2\left(a+b\right)\)
\(\Rightarrow2\left(a+b\right)-ab=0\)
\(2a+2b-ab=0\)
\(a\left(2-b\right)+2b=0\)
\(a\left(2-b\right)+2b-4=0-4\)
\(a\left(2-b\right)-2\left(2-b\right)=-4\)
\(\left(a-2\right)\left(b-2\right)=4\)
\(\Rightarrow a-2;b-2\inƯ\left(4\right)=\left\{-4;-2;-1;1;2;4\right\}\)
Do \(a,b>0\) nên ta bỏ giá trị -4 và -2
anh ơi mik giải ra mà số đo diện tích ko bằng số đo chu vi thì mik loại đúng ko anh?