Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) A = \(\dfrac{6n+7}{2n+3}\) = \(\dfrac{6n+9}{2n+3}\) − \(\dfrac{2}{2n+3}\) nguyên
⇔ 2n + 3 ∈ Ư(2) = {-2; -1; 1; 2}
⇔ 2n ∈ {-5; -4; -2; -1}
Vì n nguyên nên n ∈ {-2; -1}

a, Để 3/(n-1) nguyên
<=> 3 chia hết cho n-1
Mà n-1 nguyên
=> n-1 thuộc Ư(3)={-3,-1,1,3}
=> n=-2,0,2,4

Bài 1
Ta có:\(\left(x^2-x+a\right)\left(x+1\right)=x^3+x^2-x^2-x+ax+a=x^3-x\left(a-1\right)+a\)
Khi đó:
\(x^3+x\left(1-a\right)+a=bx^2+cx+2\)
Do đó \(1-a=c;a=2;b=0\Rightarrow a=2;b=0;c=-1\)
Bài 2:
\(A=\left(n^2+2n-5\right)\left(n+2\right)-2n^3+n+10\)
\(=n^3+2n^2+2n^2+4n-5n-10-2n^3+n+10\)
\(=-n^3+4n^2\)
\(=n^2\left(4-n\right)\)
Lập luận với n chẵn thì cái trên luôn chia hết cho 8
1. ( x2 - x + a )( x + 1 ) = x3 + bx2 + cx + 2
<=> x3 + x2 - x2 - x + ax + a = x3 + bx2 + cx + 2
<=> x3 + 0x2 + ( a - 1 )x + a = x3 + bx2 + cx + 2
<=> \(\hept{\begin{cases}b=0\\a-1=c\\a=2\end{cases}}\Leftrightarrow\hept{\begin{cases}a=2\\b=0\\c=1\end{cases}}\)
2. n chẵn => n có dạng 2k ( \(k\inℕ^∗\))
Thế vào ta được :
A = [ ( 2k )2 + 2.2k - 5 )( 2k + 2 ) - 2(2k)3 + 2k + 10
A = ( 4k2 + 4k - 5 )( 2k + 2 ) - 16k3 + 2k + 10
A = 8k3 + 16k2 - 2k - 10 - 16k3 + 2k + 10
A = -8k3 + 16k2 = -8k2(k-2) \(⋮\)8
=> A chia hết cho 8 với mọi n chẵn ( đpcm )

Bài 1:
Để \(A=\frac{a-5}{10-a}\) là số hữu tỉ dương
=> \(a-5\ge0\Rightarrow a\ge5\)
\(10-a\ge0\Rightarrow a\ge10\)
KL: a lớn hơn hoặc bằng 10 thì A là 1 số hữu tỉ dương
Bài 2: tìm n thuộc Z, để x = 2n-1/n-1 ; y = n-1/2n-1 là số nguyên ( bài 2 bn thiếu điều kiện thì phải
a) ta có: \(x=\frac{2n-1}{n-1}=\frac{2n-2+1}{n-1}=\frac{2.\left(n-1\right)+1}{n-1}=2+\frac{1}{n-1}\)
Để x nguyên
=> 1/n-1 nguyên
=> 1 chia hết cho n-1
=> n - 1 thuộc Ư(1)={1;-1}
nếu n - 1 = 1 => n = 2 (TM)
n-1 = -1 => n = 0 (TM)
KL:...
b) Để y nguyên
\(\Rightarrow\frac{n-1}{2n-1}\) nguyên
=> n - 1 chia hết cho 2n - 1
=> 2n - 2 chia hết cho 2n - 1
2n - 1 - 1 chia hết cho 2n - 1
mà 2n-1 chia hết cho 2n - 1
=> 1 chia hết cho 2n - 1
=> 2n - 1 thuộc Ư(1)={1;-1}
nếu 2n - 1 = 1 => 2n = 2 => n = 1 (TM)
2n - 1 = - 1 => 2n = 0 => n = 0 (TM)
KL:..

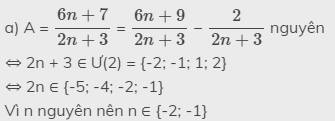
a) để x nguyên
=>13 chia hết n+2
=>n+2= 1 hoặc -1 hoặc -13 hoặc 13
=>n= -1 hoặc -3 hoặc -15 hoặc 11