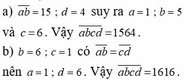Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Abcd+bcd+cd+d=8098( a,b,c khác 0 và a,b,c,d khác nhau)
Vì d x 4=….8 => d= 2 hoặc 7
Nếu d = 2 thì c x 3 = ….9 =>c=3
=> b x 2 = …0=> b= 5
Nếu b=5 => a + 1( nhớ ) = 8 => a=7
Vậy ta có số: 7532
Nếu d= 7 thì c x 3 + 2 (nhớ) = ….9 => c x 3 =…7 => c=9
b x 2 + 2 (nhớ)= …0 => b=4
a + 1(nhớ)= 8 =>a=7(loại vì a khác d)
Vậy tất cả các số thoả mãn đề bài là: 7532

=> ab00+cd+99cd=9700 hay abx100+cdx100=9700
=> (ab+cd) x 100 =9700 => ab+cd=97: trở lại bài toán tổng hiệu ta có:
ab=(97+71):2=84 => cd= 84-71=13 hay a=8,b=4,c=1,d=3;
k nha bạn ...

a) a b c d = 15; d = 4 suy ra a = 1; b = 5 và c = 6. Vậy a b c d = 1564.
b) b = 6; c = 1 có a b = c d nên a = 1; d = 6. Vậy a b c d = 1616.