
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a65b chia hết cho 45
a65b chia hết cho9;5
do a65b chia hết cho 5 => b thuộc {0;5}
TH1:b=0
(a+6+5+0)chia hết cho 9
(a+11) chia hết cho 9
0<a<9,a thuộc N
a =7
TH2:b=5
(a+6+5+5)chia hết cho 9
(a+16)chia hết cho 9
0<a<9,a thuộc N
a = 2
vậy (a,b) thuộc {(7;0);(2;5)}

lí luận hơi lủng củng, mong bn thông cảm
a. để \(\overline{6a7}\) chia hết cho 3
=>6+a+7 chia hết cho 3
=> a+13 chia hết cho 3 => a thuộc {5;8}
b. để 21a chia hết cho 5=> a = 0 hoặc a = 5
với a=0: (2+1+0) = 3; 3 chia hết cho 3 => a=0
với a=5: (2+1+5) = 8; 8 không chia hết cho 3=>a không bằng 5
vậy a=0
c. a65b chia hết cho 2;3;5;9
a65b chia hết cho 2 và 5=> b=0
ta có: a650 chia hết cho 3 và 9
=> (a+6+5+0) chia hết cho 3 và 9
=> a+11 chia hết cho 3 và 9=>a=7
d. (mình ko bt xl nha)

10.a/b = (b-a)/b
10a =b-a
11a = b
vì a/b là phân số tối giản nên a = 1 ; b = 11
Vậy phân số cần tìm là 1/11

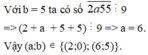
- Vì những số chia hết cho 5 có tận cùng là 0 hoặc 5
- Nên \(b=0\)hoặc \(b=5\)
- Vì những số chia hết cho 5 chỉ phụ thuộc vào số tận cùng nên:
\(\Rightarrow\)\(a\inℕ\)mà \(a\)là chữ số hàng nghìn \(\Rightarrow a\inℕ^∗\)Vậy \(a\inℕ^∗,\)\(b=0\)hoặc \(a\inℕ^∗,\)\(b=5\)
Vậy \(a\inℕ^∗,\)\(b=0\)hoặc \(a\inℕ^∗,\)\(b=5\)