TV
3
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
A
27 tháng 1 2018
Định lý Pytago: trong một tam giác vuông, tổng bình phương 2 cạnh góc vuông bằng bình phương cạnh huyền.
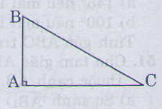
Trong một tam giác vuông, bình phương của cạnh huyền bằng tổng bình phương hai cạnh góc vuông.
∆ABC vuông tại A.
=> BC2=AB2+AC2
27 tháng 1 2018
Tham khảo nhé:
Câu hỏi của Uyên Trần - Toán lớp 7 - Học toán với OnlineMath
NH
1
23 tháng 12 2021
a: Xét ΔABD và ΔEBD có
BA=BE
\(\widehat{ABD}=\widehat{EBD}\)
BD chung
Do đó: ΔABD=ΔEBD
4 tháng 1 2017
Sống Trên Đời Mới Chỉ Là Một Nửa...♥ ♣...Biết Bao Giờ Tìm Được Nửa Thứ 2...♣ ♥..♪..♫...Trời Sinh Ra 1 + 1 = 2...♫..♪..♥ ♠..♪..♫...Cớ Sao Lại Có 2 : 2 = 1...♫..♪..♠ người buông tay ♥ 1 người ngã ♥ 1 người cất bước ♥ 1 người đau ♥ 1 người quay lưng ♥ 1 người khóc ♥ 1 người ra đi ♥ 1 người buồn ♥ 1 người đang quên ♥ 1 người nhớ ♥ 1 người hạnh phúc ♥ 1 người đau ♥ 1 người ngồi đây lòng nhung nhớ ♥ 1 người ngồi đó tựa vai ai ♥
HI
3
CW
29 tháng 5 2016
Thuận:
Trong tam giác vuông, bình phương cạnh huyền bằng tổng bình phương 2 cạnh góc vuông.
Đảo:
Tam giác có bình phương 1 cạnh bằng tổng bình phương 2 cạnh còn lại là tam giác vuông.
Có thể ko chính xác từng chữ (do lười học bài cũ), bạn thông cảm nhé ^^!
29 tháng 5 2016
Thuận:
Trong tam giác vuông, bình phương cạnh huyền bằng tổng bình phương hai cạnh góc vuông
Đảo:
Trong một tam giác, nếu có bình phương một cạnh bẳng tổng bình phương hai cạnh còn lại thì tam giác đó là tam giác vuông
Nếu mình nhớ ko nhầm thì hình như hai định lý được phát biểu như thế này. Nếu có gì sai xin các bạn thông cảm
9 tháng 6 2015
trong tam giác vuông, tổng bình phương 2 cạnh góc vuông = bình phương cạnh huyền.
ví dụ: ta có: tam giác ABC vuông tại A => AB,AC là 2 cạnh góc vuông còn cạnh BC là cạnh huyền. Thì theo Py-ta -go ta sẽ đc: \(AB^2+AC^2=BC^2\)
18 tháng 2 2017
A B C H
Ta có: \(S_{\Delta ABC}=\frac{1}{2}AB.AC=\frac{1}{2}BC.AH\)
\(\Rightarrow\frac{1}{AB.AC}=\frac{1}{BC.AH}\)
\(\Rightarrow\frac{1}{AH}=\frac{BC}{AB.AC}\)
\(\Rightarrow\frac{1}{AH^2}=\frac{BC^2}{AB^2.AC^2}=\frac{AB^2+AC^2}{AB^2.AC^2}=\frac{1}{AB^2}+\frac{1}{AC^2}\)
HN
2
NT
5 tháng 9 2017
1 . Định lý Ptago thuận
Trong một tam giác vuông, bình phương của cạnh huyền bằng tổng bình phương hai cạnh góc vuông
\(\Delta ABC\)vuông tại A
\(\Rightarrow\) BC2=AB2+AC2
2. Định lí Pytago đảo.
Nếu một tam giác có bình phương của một cạnh bẳng tổng bình phương các cạnh còn lại thì tam giác đó là tam giác vuông.
\(\Delta ABC:BC^2=AB^2+AC^2\)
\(\Rightarrow\widehat{ABC}=90^2\)
TT
2
21 tháng 3 2020
Định lý py-ta-go thuận: Trong một tam giác vuông, bình phương của cạnh huyền bằng tổng các bình phương của hai cạnh góc vuông.
Cách dùng: Dùng để tìm độ dài 1 cạnh trong tam giác vuông
Định lý py-ta-go đảo: Nếu một tam giác có bình phương của một cạnh bằng tổng các bình phương của hai cạnh kia thì tam giác đó là tam giác vuông.
Cách dùng: Dùng để chứng minh tam giác đó là tam giác vuông
!!!
21 tháng 3 2020
Py-ta-go đảo: Nếu một tam giác có bình phương của một cạnh bằng tổng các bình phương của hai cạnh kia thì tam giác đó là tam giác vuông.
Py-ta-go thuận: Theo định lý Pytago thuận, cạnh huyền của tam giác vuông thứ hai này sẽ bằng và bằng với cạnh còn lại của tam giác thứ nhất. Bởi vì cả hai tam giác có ba cạnh tương ứng cùng bằng chiều dài a, b và c, do vậy hai tam giác này phải bằng nhau. Do đó góc giữa các cạnh a và b ở tam gi
Trong một tam giác vuông, bình phương của cạnh huyền bằng tổng bình phương hai cạnh góc vuông.
∆ABC vuông tại A.
Xem thêm tại: https://loigiaihay.com/ly-thuyet-dinh-li-pytago-c42a5134.html#ixzz5ZC9Zwx7W
nhớ k mk nha ^_^
Bài làm
1. Định lì Pytago
Trong một tam giác vuông, bình phương của cạnh huyền bằng tổng bình phương hai cạnh góc vuông.
∆ABC vuông tại A.
=> BC2=AB2+AC2
2. Định lí Pytago đảo.
Nếu một tam giác có bình phương của một cạnh bẳng tổng bình phương các cạnh còn lại thì tam giác đó là tam giác vuông.
∆ABC :BC2=AB2+AC2
=> ˆBACBAC^= 902
# Chúc bạn học tốt #