Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

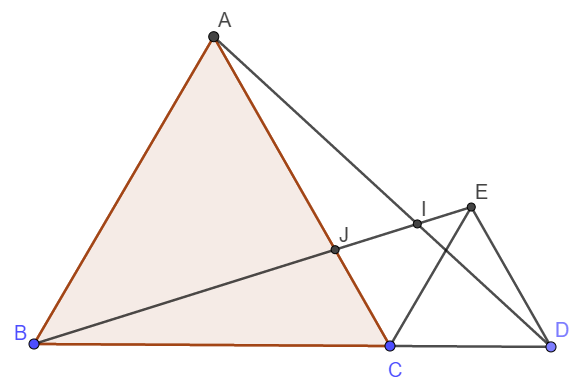
a) Do EC// AB nên \(\widehat{ECD}=\widehat{ABC}=60^o\)
Do ED// AC nên \(\widehat{EDC}=\widehat{ACB}=60^o\)
Xét tam giác ECD có \(\widehat{ECD}=\widehat{EDC}=60^o\Rightarrow\widehat{CED}=60^o\)
Suy ra ECD là tam giác đều.
b) Ta có :
\(\widehat{BCE}=\widehat{BCA}+\widehat{ACE}=60^o+\widehat{ACE}=\widehat{ECD}+\widehat{ACE}=\widehat{ACD}\)
Xét tam giác BCE và tam giác ACD có:
BC = AC (gt)
CD = CE (Do tam giác ECD đều)
\(\widehat{BCE}=\widehat{ACD}\) (cmt)
\(\Rightarrow\Delta BCE=\Delta ACD\left(c-g-c\right)\)
\(\Rightarrow BE=AC\)
c) Do \(\Delta BCE=\Delta ACD\Rightarrow\widehat{CBI}=\widehat{CAI}\)
Vậy thì \(\widehat{CBJ}+\widehat{BJC}=\widehat{JAI}+\widehat{JAI}\)
\(\Rightarrow180^o-\left(\widehat{CBJ}+\widehat{BJC}\right)=180^o-\left(\widehat{JAI}+\widehat{JAI}\right)\)
\(\Rightarrow\widehat{AIJ}=\widehat{JCB}=60^o\)
\(\Rightarrow\widehat{BID}=180^o-60^o=120^o\) (Hai góc kề bù)
\(\Rightarrow\widehat{BID}=2\widehat{BAC}\)

-tam giác cân:+2 cạnh bằng nhau, hai góc ở đáy bằng nhau
+Tam giác có đường cao kẻ từ đỉnh là phân giác(trung tuyến, trung trực)
+Tam giác có phân giác kẻ từ đỉnh là đường cao (trung trực, trung tuyến)
+Tam giác có đường trung trực kẻ từ đỉnh là phân giác (trung tuyến, đường cao)
+Tam giác có đường trung tuyến kẻ từ đỉnh là trung trực( phân giác, đường cao)
+Tam giác có một đường trung trực kẻ từ đỉnh
cm:1 tam giác là tam giác cân:
-2 cạnh bằng nhau, hai góc ở đáy bằng nhau
-Tam giác có đường cao kẻ từ đỉnh là phân giác(trung tuyến, trung trực)
-Tam giác có phân giác kẻ từ đỉnh là đường cao (trung trực, trung tuyến)
-Tam giác có đường trung trực kẻ từ đỉnh là phân giác (trung tuyến, đường cao)
- Tam giác có đường trung tuyến kẻ từ đỉnh là trung trực( phân giác, đường cao)
- Tam giác có một đường trung trực kẻ từ đỉnh
cm 1 tam giác là tam giác đều:
* tam giác đều
- chứng minh tam giác có 3 cạnh = nhau
- chứng minh tam giác có 3 góc = nhau
- chứng minh tam giác có 2 góc = 60*
- chứng minh tam giác cân có 1 góc = 60*

Vì chúng là tam giác cân có độ dài 3 cạnh bằng nhau
Nên dễ dàng áp dụng định lý Heron để tính:
\(S=18^2.\frac{\sqrt{3}}{4}=81\sqrt{3}\)
Vậy.........................

E B C M D A N
a. Xét ΔACE và ΔDCB có:
AC=DC
CE=CB
góc ACE=góc DCB (=60+gócDCE)
Suy ra : ΔACE và ΔDCB (c.g.c)
=> góc AEC=góc DBC
=> AE=DB
mà M,N lần lượt là trung điểm AE=DB
=> EM=BN
Xét ΔCME và ΔCNB có:
CE=CB
EM=BN
góc CEM=góc CBN
Suy ra : ΔCME = ΔCNB (c.g.c)
=> CM=CN ( 2 cạnh tương ứng )
=> tam giác CMN cân ở C
-> góc MCE=góc NCB
mà góc ECN+góc NCB=góc ECB=600
=> góc MCE+góc ECN=600
<=> góc MCN=600
mà tam giác MCN cân ở C
=> tam giác MNC đều (đpcm)
Không có "tam giác nửa đều" mà chỉ có "nửa tam giác đều" thôi :v
thank bn nha