Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Trả lời:
Khối lượng nước tràn ra là:
mnt = ( 260 + 28,8 ) - 276,8 = 12 (g)
Từ công thức :\(D=\frac{m}{V}\) \(\Rightarrow\) \(V=\frac{m}{D}\)
Vnt = mnt / Dnt = \(\frac{12}{1}\) = 12 ( cm3 )
Do sỏi chiếm thể tích của nước trần ra, nên ta có:
Vsỏi = 12cm3
Vậy khối lượng riêng của sỏi là:
Dsỏi = \(\frac{ms}{Vs}\) = \(\frac{28,8}{12}\) = 2,4 ( g/cm3 )
Thanks bạn nha Phạm Thùy Dung, trong mấy cái ảnh bạn tặn thì mình thích nhất cái ảnh của Kim Tae Yeon ( bạn đánh sai thành Teayon rồi đó ). Công nhận là Tea- Yeon xinh thiệt!!!![]()

Mình nghĩ là:
- Dùng cân đo khối lượng(m) của hòn đá
- Dùng bình chia độ đo thể tích(V) của hòn đá
- Dùng công thức D= m/V để tính khối lượng riêng của hòn đá

- Lần cân thứ nhất cho: mt = m b + mn + mv + m1 (1)
- Lần cân thứ hai cho: mt = m b + mn + m2 (2)
- Lần cân thứ ba cho: mt = m b + (mn – mn) + mv + m2 (3)
Từ (1) và (2) => mv = m2 – m1
Từ (1) và (3) xác định được thể tích của vật tính ra cm3. Thể tích của vật tính ra cm3 có số đo là (m3 – m1).
Vậy khối lượng riêng của vật là: m2 – m1/ m3 – m1

+) Cân thăng bằng: 2 viên bi nặng bằng nhau và đều là bi sắt. ... Giữa nút có một ống thủy tinh nhỏ, trên có khác ... +) Lần thứ nhất: Đặt lên đĩa cân bình chứa nước cất tới vạch đánh dấu, vật cần xác định thể tích, các quả cân có khối lượng tổng cộng.

Buộc vật vào sợi dây.
Treo vật vào lực kế, tìm được trọng lượng của vật là P
Nhúng vật vào bình chia, nước trong bình dâng lên là thể tích của vật, là V
Trọng lượng riêng của vật: d = P/V
Khối lượng riêng: D = d/10

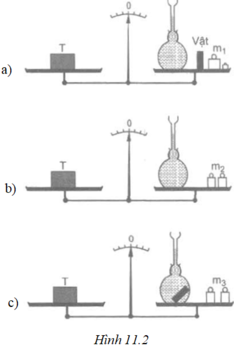
- Lần cân thứ nhất cho: mT = mb + mn + mv + m1 (1)
- Lần cân thứ hai cho: mT = mb + mn + m2 (2)
- Lần cân thứ ba cho: mT = mb + (mn – m’n) + mv + m3 (3)
Trong đó: mb là khối lượng của vỏ bình, mv là khối lượng của vật, mn là khối lượng nước trong bình khi chưa thả vật vào, m’n là khối lượng phần nước bị vật chiếm chỗ.
Từ (1) và (2) => mb + mn + mv + m1 = mb + mn + m2
⇒ mv = m2 – m1
Từ (1) và (3) => mb + mn + mv + m1 = mb + (mn – m’n) + mv + m3
⇒ m’n = m3 – m1 (g)
Vì khối lượng riêng của nước cất là 1g/cm3 nên thể tích của lượng nước mà vật chiếm chỗ là: V = m’n = m3 – m1 (cm3), đây cũng chính là thể tích của vật.
Vậy khối lượng riêng của vật là:
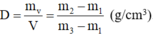

Giải
- Lần cân thứ nhất cho: mt = m b + mn + mv + m1 (1)
- Lần cân thứ hai cho: mt = m b + mn + m2 (2)
- Lần cân thứ ba cho: mt = m b + (mn – mn) + mv + m2 (3)
Từ (1) và (2) => mv = m2 – m1
Từ (1) và (3) xác định được thể tích của vật tính ra cm3. Thể tích của vật tính ra cm3 có số đo là (m3 – m1).
Vậy khối lượng riêng của vật là: m2 – m1/ m3 – m1
Lần cân thứ nhất: mT = mb + mn + mv + m1 (1).
Lần cân thứ hai: mT = mb + (mn – mn0) + mv + m2 (2).
Trong phương trình (1), mn là khối lượng của nước chứa trong bình tới vạch đánh dấu, mb là khối lượng vỏ bình, mv là khối lượng vật.
Trong phương trình (2), mn0 là khối lượng của phần nước bị vật chiếm chỗ.
Vì mT là không thay đổi nên từ (1), (2) ta có:
mb + mn + mv + m1 = mb + (mn – mn0) + mv + m2
↔ mn0 = m2 – m1.
Vì 1 gam nước nguyên chất có thể tích là 1cm3, nên số đo khối lượng mn theo đơn vị gam là số đo có thể tích của phần nước bị vật chiếm chỗ theo đơn vị cm3.
Thể tích của phần nước bị vật chiếm chỗ chính là thể tích của vật. Do đó thể tích của vật tính ra cm3 có độ lớn bằng V = m2 – m1.
* Cách xác định vật thể như trên chính xác hơn cách xác định bằng bình chia độ, đo khối lượng bằng cân Rôbécvan chính xác hơn đo thể tích bằng bình chia độ do:
+ GHĐ của cân Rôbécvan nhỏ hơn GHĐ của bình chia độ rất nhiều.
+ Cách đọc mực nước ở bình chia độ khó chính xác hơn cách theo dõi kim của cân ở vị trí cân bằng. Mặt khác, cách cân hai lần như trên loại trừ được những sai số do cân cấu tạo không được tốt, chẳng hạn hai phần của đòn cân không thật bằng nhau về chiều dài cũng như khối lượng.
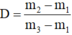
Tham KhảoCơ sở lí thuyết: d=10D ; Fas= d×V
Khi thả cầu vào trg hh, trọng lg cầu đc cân bằng với lực đẩy ac si mét của nó
Thực hiện: B1: đổ 2 dung dịch vào 1 cốc, tính v sau khi đổ
B2: Tính v của quả cầu kim loại
Nhúng quả cầu vào 1 ống đong có chứa nước. Ống dâng lên bao nhiêu thì đó là thể tích quả cầu
B3: Nhúng quả cầu đó vào hỗn hợp trên
TH1: quả cầu nửa nổi nửa chìm
Tinh phần v chìm bằng cách đánh dấu phần chìm, nhúng phần chìm đó vào ống đong có nước như B2, chỉ khác là chỉ nhúng phần mà nó chìm trong nước đa đc đánh dấu
TH2: quả cầu chìm hẳn trg nước, lơ lửng
Đã có v chìm = v cầu
TH3: cầu chạm đáy➡ tìm quả cân khác mà đo
Qua các bước trên , ta có số liệu
V chìm, trọng lượng cầu
Áp dụng ct tính lực đẩy ac si mét
F=d. V
F= P cầu
V=V chìm
➡➡➡➡➡➡➡➡d hỗn hợp
➡➡➡➡➡➡➡➡➡➡➡➡➡➡➡➡➡➡➡➡➡➡➡D hỗn hợp