Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a1, Xét tam giác AMB và tam giác AMC có :
AM chung
B=C(tam giác ABC cân )
AB=AC9tam giác ABC cân)
Do đó tam giác AMB=tam giác AMC(c.g.c)
a2, Vì tam giác AMB=tam giác AMC( cmt)
=>Bam=Cam ( 2 góc tương ứng)
=>AM là tia p/g góc A
Mình ms làm xong câu a thôi đợi mình nghĩ nót câu kia đã. bạn tick nha mình đảm bảo đúng

A B C M O I
a, xét tam giác BCO và tam giác CBI có : BC chung
góc BOC = góc CIB = 90 (Gt)
tam giác ABC cân tại A và BI; CO là đường cao => BI = CO (tc)
=> tam giác BCO = tam giác CBI (ch-cgv)
=> góc BCO = góc CBI (đn)
có góc BCO + góc OCA = góc ACB
góc CBI + góc IBA = góc ABC
góc ABC = góc ACB do tam giác ABC cân tại A (gt)
=> góc IBA = góc OCA
xét tam giác ABM và tam giác ACM có : AB = AC (tam giác ABC cân tại A)
BM = MC
=> tam giác ABM = tam giác ACM

A B C E M F D
a ) Xét \(\Delta ABM\)và \(\Delta DCB\) có :
BM = CM (gt)
\(\widehat{AMB}=\widehat{DMC}\left(đđ\right)\)
AM = DM (gt)
\(\Rightarrow\Delta ABM=\Delta DCM\left(c.g.c\right)\)
Vì : \(\Delta ABM=\Delta DCM\left(cmt\right)\)
\(\Rightarrow\widehat{ABM}=\widehat{DCM}\) . Mà 2 góc này ở vị trí so le trong
\(\Rightarrow\) AB // DC
c ) Xét \(\Delta EBM\) và \(\Delta FCM\) có :
\(\widehat{BEM}=\widehat{CFM}=90^o\)
BM = MC (gt)
\(\widehat{BME}=\widehat{CMF}\left(đđ\right)\)
\(\Rightarrow\Delta EBM=\Delta FCM\)(cạnh huyền - góc nhọn )
\(\Rightarrow ME=MF\)
\(\Rightarrow M\) là trung điểm của EF ( đpcm)
Chúc bạn học tốt !!!
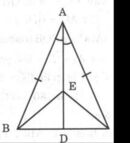




xin sửa lại đề bài toán câu a cho a bn A) tam giác ABM=tam giác ACM
A)vì AB=AC nên tam giác ABC cân tại A
vì tam giác ABC cân tại A nên ABC = ACB
Xét tam giác ABM và tam giác ACM
MAB=MAC
AB=AC
ABM=ACM
Suy ra tam giác ABM = tam giác ACM (G.C.G)
B) vì tam giác ABM=tam giác ACM (câu a) nên BM=MC (2 cạnh t.ư)
suy ra M là tđ của BC
Vì tam giác ABM= tam giác ACM (câu a) nên AMB=AMC
ta có : AMB + AMC =180ĐỘ ( 2 góc kề bù)
nên AMB = AMC = 180độ :2 =90độ
suy ra AM vuông góc BC