
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


- Hầu như các OLmers toàn tầm khoảng 2k4 đến 2k9 nên mk nghĩ là câu này của bn khó cs ai TL đc =))
- Mk nghĩ bn nên vào web : H để đăng bài ! Vì mk thấy ở đó chuyên giải mấy bài khó -,-
- Hoăc bn cs thể nhờ https://olm.vn/thanhvien/linhchi_nguyenthi1997 ( cj này là quản lý của olm và hay giải mấy bài khó )
Ckuc bn hok tốt =))

đáp án:
Hàm số đã cho xác định trên D = R.
Với m = -1. Khi đó hàm số trở thành y = -2x + 4 ; y' = -2 < 0 ∀x∈R, không thỏa mãn yêu cầu bài toán.
Với m ≠ -1. Ta có f'(x)= 3(m+1)x2 - 6(m + 1)x + 2m
+ Hàm số đồng biến trên khoảng có độ dài không nhỏ hơn 1 khi và chỉ khi f'(x) = 0 có hai nghiệm phân biệt x1,x2 và hàm số đồng biến trong đoạn [x1;x2 ] thỏa mãn |x1 - x2 | ≥ 1
+ f'(x)= 0 có hai nghiệm phân biệt x1,x2 và hàm số đồng biến trong đoạn[x1;x2]
Theo Viét ta có
+ Với |x1 - x2 | ≥ 1 ⇔ (x1 + x2 )2 - 4x1 x2 - 1 ≥ 0
Đối chiếu điều kiện ta có m ≤ -9.

\(VT=\left|x-\left(-y+\frac{1}{100}\right)\right|\ge\left|x\right|-\left|-y+\frac{1}{100}\right|\)
\(\ge\left|x\right|-\left(\left|-y\right|+\left|\frac{1}{100}\right|\right)=\left|-x\right|-\left|y\right|-\left|\frac{1}{100}\right|=VP\)
Dấu "=" xảy ra khi \(\hept{\begin{cases}\left|x\right|\ge\left|-y+\frac{1}{100}\right|\\x\left(-y+\frac{1}{100}\right)\ge0\\-y.\frac{1}{100}\ge0\end{cases}}\Leftrightarrow\hept{\begin{cases}x+y\ge\frac{1}{100}\\x\ge\frac{1}{100}\\y\le0\end{cases}}\)
Vậy pt có nghiệm \(x\ge\frac{1}{100};y\le0\) thoả mãn \(x+y\ge\frac{1}{100}\)

ღᏠᎮღĐiền❤RaiBo༻꧂
Phải giải chi tiết ra chứ, bài dễ mak, lớp 6 cx lm đc


\(x^{2019}-y^{2019}+2\left(x-y\right)=0\)
<=> \(\left(x-y\right)\left(x^{2018}+x^{2017}y+...+xy^{2017}+y^{2018}\right)+2\left(x-y\right)=0\)
<=> \(\left(x-y\right)\left(x^{2018}+x^{2017}y+...+xy^{2017}+y^{2018}+2\right)=0\)(1)
Có: \(x^{2018}+x^{2017}y+...+xy^{2017}+y^{2018}+2>0\)mọi x, y.
(1) <=> \(x-y=0\)
<=> x = y
Thế vào P ta có:
\(P=x^4-2x^2+2=\left(x^2-1\right)^2+1\ge1\)
"=" xảy ra <=> \(y=x=\pm1\)
Vậy min P =1 khi và chỉ khi x = y =1 hoặc x = y =-1.
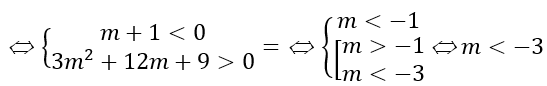
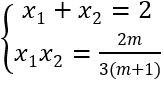
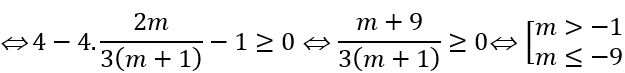
\(4^x+80=5^y\left(1\right)\)
+) Với \(x=0\)thay vào (1) ta được :
\(4^0+80=5^y\)
\(81=5^y\)( loại )
+) Với \(x=1\)thay vào(1) ta được:
\(4^1+80=5^y\)
\(84=5^y\)( loại )
+) Với x>1 ta có: \(4^x\)có tận cùng là hoặc 6 nên \(4^x+80\) sẽ có tận cùng là 4 hoặc 6
Mà \(5^y\)luôn có chữ số tận cùng là 5
\(\Rightarrow\)mâu thuẫn
\(\Rightarrow x>1\)loại
Vậy ko có giá trị x,y nào
dòng thứ 5 từ dưới lên trên
Mình ghi thiếu là chỗ \(4^x\)có tận cùng là 4 hoặc 6