Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(S=\frac{1}{a^2+b^2}+\frac{25}{ab}+ab\)
\(=\left(\frac{1}{a^2+b^2}+\frac{1}{2ab}\right)+\left(ab+\frac{16}{ab}\right)+\frac{17}{2ab}\)
\(\ge\frac{4}{\left(a+b\right)^2}+2\sqrt{ab\cdot\frac{16}{ab}}+\frac{17}{\frac{\left(a+b\right)^2}{2}}\)
\(\ge\frac{4}{4^2}+8+\frac{17}{\frac{4^2}{2}}=\frac{83}{8}\)
Dấu "=" xảy râ khi x = y = 2
Ta có \(a+b\ge2\sqrt{ab}\)=> \(ab\le4\)
\(\frac{1}{a^2+b^2}+\frac{1}{2ab}\ge\frac{4}{\left(a+b\right)^2}\ge\frac{1}{4}\)
\(\frac{16}{ab}+ab\ge8\)
\(\frac{17}{2ab}\ge\frac{17}{8}\)
=> \(S\ge8+\frac{17}{8}+\frac{1}{4}=\frac{83}{8}\)
Vậy MinS=83/8 khi a=b=2

Áp dụng bất đẳng thức Cosi ta có :
\(4\ge a+b\ge2\sqrt{ab}\Leftrightarrow\sqrt{ab}\le2\Leftrightarrow ab\le4\)
Ta có bất đẳng thức \(\frac{1}{x}+\frac{1}{y}\ge\frac{4}{x+y}\)
(Nhân chéo để chứng minh )
Áp dụng :
\(S=\frac{1}{a^2+b^2}+\frac{25}{ab}+ab=\frac{1}{a^2+b^2}+\frac{1}{2ab}+\frac{49}{2ab}+ab\)
\(=\frac{1}{a^2+b^2}+\frac{1}{2ab}+ab+\frac{16}{ab}+\frac{17}{2ab}\)
\(\ge\frac{4}{a^2+b^2+2ab}+2\sqrt{ab.\frac{16}{ab}}+\frac{17}{2ab}\)
\(\ge\frac{4}{\left(a+b\right)^2}+8+\frac{17}{2.4}=\frac{1}{4}+8+\frac{17}{8}=\frac{83}{8}\)
Dấu " = " xảy ra \(\Leftrightarrow a=b=2\)

Đang rảnh, làm luôn\(A=\dfrac{a}{bc}+\dfrac{b}{ca}+\dfrac{c}{ab}=\dfrac{1}{2}\left[\left(\dfrac{a}{bc}+\dfrac{b}{ca}\right)+\left(\dfrac{b}{ca}+\dfrac{c}{ab}\right)+\left(\dfrac{c}{ab}+\dfrac{a}{bc}\right)\right]\ge\dfrac{1}{2}\left(\dfrac{2}{c}+\dfrac{2}{a}+\dfrac{2}{b}\right)=\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}=\dfrac{3}{2}\)
Dấu "=" xảy ra <=> a = b = c = 2

Chào bạn, mình từng làm bài này giúp một bạn khác rồi, link đây nhé:
https://hoc24.vn/hoi-dap/question/778686.html

Câu a dùng hằng đẳng thức mở rộng là được,tối rồi lười lắm,t giúp câu b
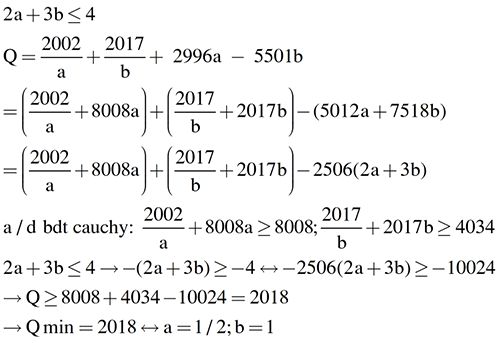
\(A=\left(\dfrac{1}{a^2+b^2}+\dfrac{1}{2ab}\right)+\left(ab+\dfrac{16}{ab}\right)+\dfrac{17}{2ab}\)
\(A\ge\dfrac{4}{a^2+b^2+2ab}+2\sqrt{\dfrac{16ab}{ab}}+\dfrac{17}{\dfrac{2\left(a+b\right)^2}{4}}\)
\(A\ge\dfrac{4}{\left(a+b\right)^2}+8+\dfrac{34}{\left(a+b\right)^2}\ge\dfrac{4}{4^2}+8+\dfrac{34}{4^2}=\dfrac{83}{8}\)
Dấu "=" xảy ra khi \(a=b=2\)