Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi số máy cày của ba đội lần lượt là x, y, z (máy)
Vì diện tích cày là như nhau nên số máy cày và thời gian là hai đại lượng tỉ lệ nghịch
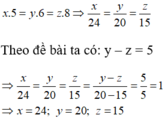
Chọn đáp án A

Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{a}{10}=\dfrac{b}{6}=\dfrac{c}{5}=\dfrac{b-c}{6-5}=1\)
Do đó: a=10; b=6; c=5

Gọi số máy cày của 3 đọi lần lượt là: a;b;c (máy)
Với cùng 1 diện tích đất thì số máy cày và thời gian làm xong việc là 2 ĐLTLN; ta có:
a3=b5=c6=>a/(1/3)=b/(1/5)=c/(1/6) và b-c=1
ttcdtsbn; ta có:
a/(1/3)=b/(1/5)=c/(1/6)=(b-c)/(1/5-1/6)=1/(1/30)=30
Khi đó: a=10; b=6; c=5
Vậy số máy của 3 đội lần lượt là 10;6;5
Gọi số máy cày của 3 đọi lần lượt là: a;b;c (máy)
Với cùng 1 diện tích đất thì số máy cày và thời gian làm xong việc là 2 ĐLTLN; ta có:
a3=b5=c6=>a/(1/3)=b/(1/5)=c/(1/6) và b-c=1
ttcdtsbn; ta có:
a/(1/3)=b/(1/5)=c/(1/6)=(b-c)/(1/5-1/6)=1/(1/30)=30
Khi đó: a=10; b=6; c=5
Vậy số máy của 3 đội lần lượt là 10;6;5

Gọi số máy mỗi đội lần lượt có là: a,b,c ( máy ) ( a,c,b \(\in\)N* , b > 1 )
Theo bài ra , ta có : b - c = 1
Vì số máy tỉ lệ nghịch với số ngày nên: 3a = 5b= 6c
\(\Rightarrow\frac{a}{\frac{1}{3}}=\frac{b}{\frac{1}{5}}=\frac{c}{\frac{1}{6}}=\frac{b-c}{\frac{1}{5}-\frac{1}{6}}=\frac{1}{\frac{1}{30}}=30\)
\(\Rightarrow\hept{\begin{cases}a=30.\frac{1}{3}=10\\b=30.\frac{1}{5}=6\\c=30.\frac{1}{6}=5\end{cases}}\)
Vậy sô máy của 3 đội lần lượt là 10 ; 6 ; 5 máy.
gọi số máy cày của 3 đội lần lướt là a , b , c.
theo bài ra,ta có : b-c=1
vì số máy cày tỉ lệ nghịch với số ngày hoàn thành công việc nên ,ta có:
a/1/3=b/1/5=c/1/6
áp dụng tính chất dãy tỉ số bằng nhau , ta có
a/1/3=b/1/5=c/1/6=b-c/1/5-1/6=1/1/30
=> a=30 nhân\(\frac{1}{3}\)= 10
b=30 nhân \(\frac{1}{5}\)=6
c=30 nhân \(\frac{1}{6}\)=5
vậy đọi 1 có 10 máy
đội 2 có 6 máy
đọi 3 có 5 máy

Gọi x (máy), y (máy), z (máy) lần lượt là số máy cày của các đội 1, 2, 3 (điều kiện x, y, z ∈ N*)
Vì diện tích các cánh đồng là như nhau nên số máy cày và số ngày hoàn thành công việc là hai đại lượng tỉ lệ nghịch, suy ra 3x = 5y = 6z.
Đội thứ hai nhiều hơn đội thứ ba 1 máy nên y – z = 1.
Từ 3x = 5y = 6z, suy ra
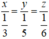
Áp dụng tính chất của dãy tỉ số bằng nhau ta có:
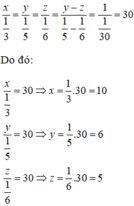
Vậy đội 1 có 10 máy cày, đội hai có 6 máy và đội 3 có 5 máy

Gọi số máy của đội 1;2;3 lần lượt là a,b,c
Theo đề, ta có: 3a=5b=6c và a-c=5
=>a/10=b/6=c/5 và a-c=5
Áp dụng tính chất của DTSBN, ta được:
\(\dfrac{a}{10}=\dfrac{b}{6}=\dfrac{c}{5}=\dfrac{a-c}{10-5}=1\)
=>a=10; b=6; c=5

Giải:
Gọi số máy cày của mỗi đội lần lượt là a, b, c.
Vì số máy cày và số ngày làm việc tỉ lệ nghịch với nhau nên ta có:
\(a.3=b.5=c.6\) và \(b-c=1\)
\(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{a}{5}=\dfrac{b}{3}\\\dfrac{b}{6}=\dfrac{c}{5}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{a}{10}=\dfrac{b}{6}\\\dfrac{b}{6}=\dfrac{c}{5}\end{matrix}\right.\Leftrightarrow\dfrac{a}{10}=\dfrac{b}{6}=\dfrac{c}{5}\)
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
\(\Leftrightarrow\dfrac{a}{10}=\dfrac{b}{6}=\dfrac{c}{5}=\dfrac{b-c}{6-5}=\dfrac{1}{1}=1\)
\(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{a}{10}=1\\\dfrac{b}{6}=1\\\dfrac{c}{5}=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=10\\b=6\\c=5\end{matrix}\right.\)
Vậy số máy cày của mỗi đội lần lượt là 10 máy, 6 máy và 5 máy.
Giải :
Gọi a,b,c là số máy cày lần lượt tỉ lệ với các số 3,5,6 và b - c = 2
Vì số máy cày và số ngày làm việc là hai đại lượng tỉ lệ nghịch nên ta có :
a/1/3 = b/1/5 = c/1/6 = b/1/5 - c/1/6 = 2/1/30 = 60
Do đó :
a/1/3 = 60 => a = 60.1/3 = 20
b/1/5 = 60 => b = 60.1/5 = 12
c/1/6 = 60 => c = 60.1/6 =10
Vậy số máy cày của ba đội lần lượt là : 20 ; 12 ; 10
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{a}{\dfrac{1}{3}}=\dfrac{b}{\dfrac{1}{5}}=\dfrac{c}{\dfrac{1}{6}}=\dfrac{b-c}{\dfrac{1}{5}-\dfrac{1}{6}}=30\)
Do đó: a=10; b=6; c=5