Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: Xét ΔABC có
BN là đường trung tuyến
AM là đường trung tuyến
BN cắt AM tại G
Do đó: G là trọng tâm của ΔABC
=>AG=2GM
mà AG=GG'
nên GG'=2GM
=>M là trung điểm của GG'
b: Xét tư sgiác BGCG' có
M là trung điểm của BC
M là trung điểm của GG'
Do đó: BGCG' là hình bình hành
Suy ra: CG=BG' và CG//BG'

1)
xét ΔAEK và Δ CEG có:
EA=EC(gt)
EG=EK(gt)
góc AEK= góc GEC( 2 góc đối đỉnh)
=> ΔAEK=ΔCEG(c.g.c)
=> AK=GC
cm tương tự ta có:ΔGDC=ΔIDB(c.g.c)
=> GC=BI
và AK=GC
=> AK=GC=BI
2)
theo câu a, ta có ΔAEK=ΔCEG(c.g.c)
=> góc EAK= góc ECG
=> AK//GC
theo câu a, ta có: ΔGDC=ΔIDB(c.g.c)
=> góc DGC= góc DIB
=> GC//BI
và AK//GC
=> AK//BI
3)
ta có: AD là đường trung tuyến ứng với cạnh BC của Δ ABC
BE là đường trung tuyến ứng với cạnh AC của ΔABC
=> giao của AD và BE là trọng tâm của ΔABC
=> G là trọng tâm của ΔABC
=> GA=2GD
mà GI=ID
=> GA=GI+ID=GI
ta có G là trọng tâm của ΔABC; BE là đường trung tuyến của ΔABC
=> BG=2GE
mà GE=EK
=> BG=GE+EK=GK
xét ΔGAK và ΔGIB có :
GA=GI(cmt)
GK=GB(cmt)
góc AGK= góc BGI(2 góc đối đỉnh)
=>ΔGAK=ΔGIB(c.g.c)
4)
ta có AD là đường trung tuyến của ΔABC
=> AD=3GD
hay DG=DA:3
ta có : BE là đường trung tuyến của ΔABC
=> GE=BE:3
5)
nếu CF là đường trung tuyến của ΔABC cắt AD tại G thì G là trọng tâm của tam giác ΔABC( tương tự như câu 4)
=> CG=2GF
NX: 3 đường trung tuyến của 1 tam giác cắt nhau tại 1 điểm. điểm này gọi là trọng tâm của tam giác đó
điểm này cách trung điểm của cạnh mà đoạn thẳng đi qua nó một khoảng =1/2 k/cách từ điểm đó đến đỉnh của tam giác mà đoạn thẳng đã đi nó

a, Xét tam giác ABC có G là trọng tâm
=> \(PG=\frac{1}{3}PC\) ( t/c trọng tâm tam giác )
Xét tam giác ABG có GP và AF là các trung tuyến
Mà GP cắt AF tại I nên I là trọng tâm
=> \(PI=\frac{1}{3}PG=\frac{1}{3}\cdot\frac{1}{3}PC=\frac{1}{9}PC\) ( đpcm )

Bài làm
Ta có: \(AG=\frac{2}{3}AM\)
\(CG=\frac{2}{3}CP\)
\(BG=\frac{2}{3}BN\)
Mà AG = BG = CG
=> \(\frac{2}{3}AM=\frac{2}{3}CP=\frac{2}{3}BN\)
=> \(AM=CP=BN\)
Vì AG = GC ( gt )
=> Tam giác AGC cân tại G
Mà BN là đường trung tuyến và G thuộc BN
=> GN cũng là đường trung tuyến
=> GN là đường cao ( do tam giác AGC cân ở G )
=> Tam giác ABC cân ở B
=> AB = BC (1)
Vì AG = GB ( gt )
=> Tam goác AGB cân tại G
Mà CP là đường trung tuyến và G thuộc CP
=> GN là đường trung tuyến
Và GN cũng là đường trung tuyến của tam giác cân AGC
=> GN cũng là đường cao
=> CP cũng là đường cao.
=> Tam giác ACB cân ở C
=> AC = BC (2)
Vì BG = GC ( gt )
=> Tam giác BGC cân tại G
Mà AM là đường trung tuyến và G thuộc AM
=> GM cũng là đường trung tuyến của tam giác GBC
Và GM là đường cao
=> AM cũng là đường cao
=> Tam giác ABC cân ở A
=> AB = AC (3)
Từ (1) và (2) và (3) => AB = AC = BC
=> Tam giác ABC đều.
# Học tốt #
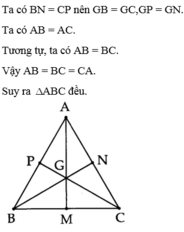
A B C N P M G
Ta có: AG = GB (gt) => t/giác AGB cân tại G có GN là đường trung tuyến
=> GN cũng là đường cao của t/giác AGB
Hay CN là đường cao của t/giác ABC (Do C, G, N
| | |)mà CN cũng là đường trung tuyến
=> t/giác ACB cân tại C => AC = CB (1)
BG = GC (gt) => t/giác BGC cân tại G có GM là đường trung tuyến
=> GM cũng là đường cao của t/giác GBC
hay AM là đường cao của t/giác ABC (Do A; G; M
| | |)mà AM cũng là đường trung tuyến của t/giác ABC
=> t/giác ABC cân tại A => AB = AC (2)
Từ (1) và (2) => AB = AC = BC
=> t/giác ABC đều