

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




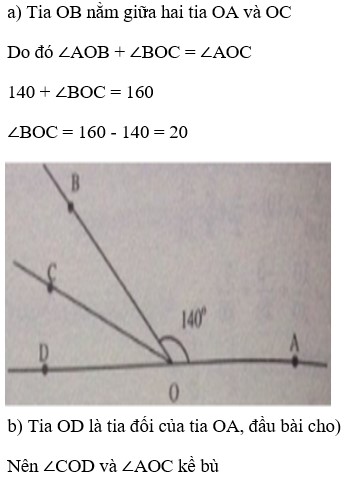
\(\widehat{AOB}\)= \(140^o\)
\(\widehat{AOC}\)= \(160^o\)
Nên để tính góc \(\widehat{BOC}\)ta lấy
\(\widehat{AOC}\)- \(\widehat{AOB}\) = \(160^o\)- \(140^o\) = \(20^o\)
\(\widehat{BOC}\) = \(20^o\)
Góc COD :
AOD đối nhau nên góc \(\widehat{AOD}\)= \(180^o\)
Rồi ta lấy góc \(\widehat{AOD}\)- \(\widehat{AOC}\)= \(180^o\) - \(160^o\) = \(20^o\)
\(\widehat{COD}\) = \(20^o\)
Tia OC là tia phân giác của góc \(\widehat{BOD}\)
VÌ tia OC nằm giữa góc \(\widehat{BOD}\)
CHÚC BẠN THÀNH CÔNG

b,giải thích dài lắm phải chứng minh các tia nằm giữa sau đó mới có thể kết luận. Sau đó tìm tia nào có quan hệ với tia cần đáp án cần tìm
c,Các tia đối nhau có tổng số đo =90 độ. Bạn phải xét trên 2 tia thì mới tính dc
a,90 độ
Mk gợi ý thôi. Còn đâu phải tự làm cho đỡ lười
O x z y a B C
(Tự đánh dấu góc)
a) Trên cùng 1 nửa MP bờ chứa tia Ox, có xOy < xOz ( 30o<120o)
=> Oy nằm giữa Ox, Oz
=> yOz + xOy = xOz => yOz = 90o
b) Trên cùng 1 nửa MP bờ chứa tia Ox có : xOy < xOa ( 30o < 75o)
=> Oy nằm giữa Ox,Oa
=> xOy + aOy = xOa => aOy = 45o
Vì Oa nằm trong yOz => Oa nằm giữa Oy,Oz
=> aOy + aOz = yOz => aOz = 45o
Có : Oa nằm giữa Oy,Oz
aOz = aOy = 45o => Oa là p/g của yOz
c) Ob là tia đối Oy
=> bOz và yOz kề bù
=> bOz + yOz = 180o => bOz = 90o
Oc là tia đối của Oz => zOc là góc bẹt => zOc = 180o
Trên cùng 1 nửa MP bờ chứa Oz có bOz < zOc ( 90o <180o)
=> Ob nằm giữa Oz, Oc
=> bOz + bOc = zOc => bOc = 90o

a) tia Ob nằm giữa Oa và Ob vì :
^aOb+^bOc=^aOc
^aOb<^bOc(600<1200)
b) VìtiaObnằm giữa OavàOcnên:
^aOb+^bOc=^aOc
600+ ^bOc=1200
^bOc=1200−600
⇒ ^bOc=600
TiaOblàtiaphângiaccua^aOcvì:
^aOb+^bOc=^aOc
^aOb=^bOc=1600
P/s : bạn vào câu hỏi tương tự để xem thêm nhé !
a,Vì ^AOB < ^AOC (60o < 120o)
=>OB nằm giữa OA và OC (1)
b,Ta có ^AOB + ^BOC = ^AOC
60o + ^BOC = 120o
^BOC = 60o
=>^AOB = ^BOC = 60o (2)
Từ (1) và (2)=>Ob là p/g ^AOC
c,TA có ^AOC + ^COD = 180o(góc bẹt)
=>^COD=180o - 120o
=>^COD=60o
=> ^COE=^EOD=\(\frac{60^o}{2}=30^o\)
Ta có: ^EOB=^BOC + ^COE
^EOB=60o + 30o
^EOB= 90o

O A B x y C E D
a. AB= AO+OB
=3+2
=5
Vậy: AB=5cm
b. Vì \(\widehat{BOC}< \widehat{BOE}\)=> OC là tia nằm giữa 2 tia OE và OB và vì \(\widehat{BOC}=50^0=\widehat{BOE}:2=100^0:2\)
=> OC là tia phân giác của \(\widehat{BOE}\)
c. \(\widehat{COD}=\widehat{COE}+\widehat{EOD}\)
\(=\left(\widehat{BOE}:2\right)+\left(\widehat{EOA}:2\right)\)
\(=\left(100^0:2\right)+\left(\widehat{AOB}-\widehat{EOB}\right):2\)
\(=50^0+\left(180^0-100^0\right):2\)
\(=50^0+80^0:2\)
\(=50^0+40^0=90^0\)
=> \(\widehat{COD}=90^0\)
Vậy: \(\widehat{COD}\)là góc vuông
k cho mik nha

ta có: góc AOB , góc COB kề bù
=> OB nằm giữa OA, OC
=> góc AOC = 180 độ
mà OD,OB nằm cùng trên một nửa mặt phẳng bờ AC
=> OD nằm giữa OA,OC
=> góc AOD + góc COD = góc AOC
thay số: 80 độ + góc COD = 180 độ
góc COD = 180 độ - 80 độ
góc COD = 100 độ
b) ta có: OD,OB nằm trên cùng một nửa mặt phẳng bờ là OC ( hay AC)
mà góc COB < góc COD ( 50 độ < 100 độ)
=> OB nằm giữa OD, OC (1)
=> góc COB + góc DOB = góc COD
thay số: 50 độ + góc DOB = 100 độ
góc DOB = 100 độ - 50 độ
góc DOB = 50 độ
=> góc COB = góc DOB = góc COD/2 ( = 50 độ) (2)
Từ (1);(2) => OB là tia phân giác góc COD