Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Câu a) đúng. Khoảng cách của hai đường thẳng chéo nhau là đoạn ngắn nhất trong các đoạn thẳng nối hai điểm bất kì nằm trên hai đường thẳng ấy và ngược lại (xem mục c). Tính chất của khoảng cách giữa hai đường thẳng chéo nhau (Bài 5 – chương III).
Câu b) sai. Qua một điểm có vô số mặt phẳng vuông góc với một mặt phẳng cho trước.
Câu c) sai. Vì trong trường hợp đường thẳng vuông góc với mặt phẳng thì ta có vô số mặt phẳng vuông góc với mặt phẳng cho trước vì bất kì mặt phẳng nào chứa đường thẳng cũng đều vuông góc với mặt phẳng cho trước. Để có khẳng định đúng ta phải nói: Qua một đường thẳng không vuông góc với một mặt phẳng có duy nhất một mặt phẳng vuông góc với mặt phẳng đã cho.
Câu d) sai. Vì đường vuông góc chung của hai đường thẳng phải cắt cả hai đường ấy.

Câu a) đúng. Khoảng cách của hai đường thẳng chéo nhau là đoạn ngắn nhất trong các đoạn thẳng nối hai điểm bất kì nằm trên hai đường thẳng ấy và ngược lại (xem mục c). Tính chất của khoảng cách giữa hai đường thẳng chéo nhau (Bài 5 – chương III).
Câu b) sai. Qua một điểm có duy nhất một mặt phẳng vuông góc với một mặt phẳng cho trước.
Câu c) sai. Vì trong trường hợp đường thẳng vuông góc với mặt phẳng thì ta có vô số mặt phẳng vuông góc với mặt phẳng cho trước vì bất kì mặt phẳng nào chứa đường thẳng cũng đều vuông góc với mặt phẳng cho trước. Để có khẳng định đúng ta phải nói: Qua một đường thẳng không vuông góc với một mặt phẳng có duy nhất một mặt phẳng vuông góc với mặt phẳng đã cho.
Câu d) sai. Vì đường vuông góc chung của hai đường thẳng phải cắt cả hai đường ấy.

Khẳng định (1) đúng vì khoảng cách của hai đường thẳng chéo nhau là đoạn ngắn nhất trong các đoạn thẳng nối hai điểm bất kì nằm trên hai đường thẳng ấy và ngược lại (xem mục c). Tính chất của khoảng cách giữa hai đường thẳng chéo nhau (Bài 5 – chương III).
Khẳng định (2) sai vì qua một điểm có vô số mặt phẳng vuông góc với một mặt phẳng cho trước.
Khẳng định (3) sai vì trong trường hợp đường thẳng vuông góc với mặt phẳng thì ta có vô số mặt phẳng vuông góc với mặt phẳng cho trước vì bất kì mặt phẳng nào chứa đường thẳng cũng đều vuông góc với mặt phẳng cho trước. Để có khẳng định đúng ta phải nói: Qua một đường thẳng không vuông góc với một mặt phẳng có duy nhất một mặt phẳng vuông góc với mặt phẳng đã cho.
Khẳng định (4) sai vì đường vuông góc chung của hai đường thẳng phải cắt cả hai đường ấy.
Vậy có một khẳng định đúng.
ĐÁP ÁN A

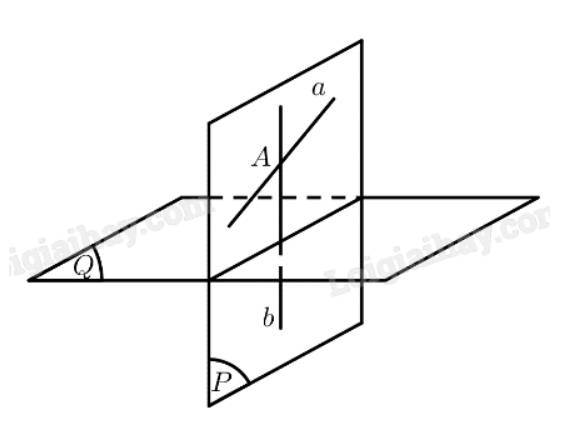
Cho đường thẳng \(a\) không vuông góc với mặt phẳng \(\left( Q \right)\). Ta cần chứng minh tồn tại duy nhật mặt phẳng \(\left( P \right)\) chứa đường thẳng \(a\) và vuông góc với mặt phẳng \(\left( Q \right)\).
• Lấy điểm \(A \in a\). Qua điểm \(A\) kẻ đường thẳng \(b\) vuông góc với mặt phẳng \(\left( Q \right)\).
\(\left. \begin{array}{l}b \bot \left( Q \right)\\b \in mp\left( {a,b} \right)\end{array} \right\} \Rightarrow mp\left( {a,b} \right) \bot \left( Q \right)\)
Vậy tồn tại mặt phẳng chứa đường thẳng \(a\) và vuông góc với mặt phẳng \(\left( Q \right)\).
• Giả sử có thêm mặt phẳng \(\left( P \right)\) chứa đường thẳng \(a\) và vuông góc với mặt phẳng \(\left( Q \right)\).
\( \Rightarrow a = \left( P \right) \cap mp\left( {a,b} \right)\)
Theo Bài tập 3b trang 99 ta có \(a \bot \left( Q \right)\), trái với giả thiết \(a\) không vuông góc với mặt phẳng \(\left( Q \right)\).
Vậy \(\left( P \right) \equiv mp\left( {a,b} \right)\).
a) Sai
b) Sai
c) Đúng
d) Sai