Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Hướng dẫn:
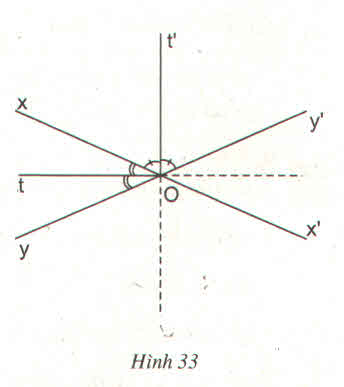
a) Vì Ot là phân giác của ˆxOyxOy^
nên ˆyOtyOt^ = ˆxOtxOt^ = 1212ˆxOyxOy^
Ot' là phân giác của ˆxOy′xOy′^
nên ˆxOt′xOt′^ = ˆy′Ot′y′Ot′^ = 1212ˆxOy′xOy′^
=> ˆxOtxOt^ + ˆxOt′xOt′^ = 1212ˆxOyxOy^ + 1212ˆxOy′xOy′^ = 1212(ˆxOyxOy^ + ˆxOy′xOy′^)
mà (ˆxOyxOy^ + ˆxOy′xOy′^) = 1800 (2 góc kề bù)
=> ˆxOtxOt^ + ˆxOt′xOt′^ = 12121800 = 900
Vậy hai tia phân giác của hai góc kề bù tạo thành một góc vuông
b) Nếu M thuộc Ot hoặc Ot' thì M cách đều hai đường thẳng xx' và yy'
Thật vậy: M ε Ot do Ot là phân giác của ˆxOyxOy^ nên M cách đều Ox, Oy
=> M cách đều xx',yy'
M ε Ot'do Ot' là phân giác của ˆxOy′xOy′^ nên M cách đều xx', yy'
=> M cách đều xx',yy'
c) M cách đều hai đường thẳng xx', yy'
Nếu M nằm trong một góc trong bốn góc ˆxOyxOy^, ˆxOy′xOy′^, ˆx′Oy′x′Oy′^, ˆx′Oyx′Oy^ thì M phải thuộc phân giác của góc ây tức M phải thuộc Ot hoặc Ot'
d) Khi M ≡ O thì khoảng cách từ M đến xx', yy' bằng 0
e) Từ các câu trên ta có nhận xét: Tập hợp tất cả các điểm cách đều hai đường thẳng cắt nhau xx', yy' thuộc hai đường thẳng vuông góc nhau lần lượt là phân giác của các góc tạo bởi hai đường thẳng cắt nhau đó.
a) Vì Ot là phân giác của ˆxOyxOy^
nên ˆyOtyOt^ = ˆxOtxOt^ = 1212ˆxOyxOy^
Ot' là phân giác của ˆxOy′xOy′^
nên ˆxOt′xOt′^ = ˆy′Ot′y′Ot′^ = 1212ˆxOy′xOy′^
=> ˆxOtxOt^ + ˆxOt′xOt′^ = 1212ˆxOyxOy^ + 1212ˆxOy′xOy′^ = 1212(ˆxOyxOy^ +

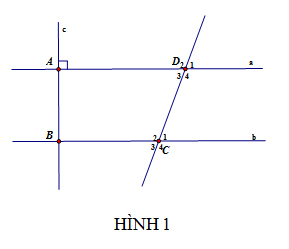
trc hết D1= 70O
a) D1 = D3= 70 (đối đỉnh)
C2 + D3 = 110+70 = 180 ( 2 góc này ở
vị trí trong cùng phía) nên a//b
b) theo a) có a//b
mà c vuông góc với a => c vuong goc voi b

Hướng dẫn:
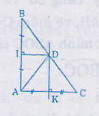
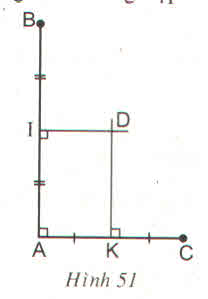
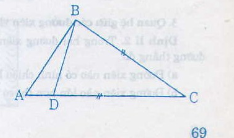
Từ hình vẽ ta có:
DK là trung trực của Ac, DI là đường trung trực của AB. Do đó ∆ADK = ∆CDK (c.c.c)
=> ˆADK=ˆCDKADK^=CDK^
hay DK là phân giác ˆADCADC^
=> ˆADKADK^ = 1212ˆADCADC^
∆ADI = ∆BDI (c.c.c)
=> ˆADI=ˆBDIADI^=BDI^
=> DI là phân giác ˆADBADB^
=> ˆADIADI^ = 1212 ˆADBADB^
Vì AC // DI ( cùng vuông góc với AB) mà DK ⊥ AC
=> DK ⊥ DI
hay ˆADKADK^ + ˆADIADI^ = 900
Do đó 1212ˆADCADC^ + 1212 ˆADBADB^ = 900
=> ˆADCADC^ + ˆADBADB^ = 1800

Từ hình vẽ ta có:
DK là trung trực của Ac, DI là đường trung trực của AB. Do đó ∆ADK = ∆CDK (c.c.c)
=> ˆADK=ˆCDKADK^=CDK^
hay DK là phân giác ˆADCADC^
=> ˆADKADK^ = 1212ˆADCADC^
∆ADI = ∆BDI (c.c.c)
=> ˆADI=ˆBDIADI^=BDI^
=> DI là phân giác ˆADBADB^
=> ˆADIADI^ = 1212 ˆADBADB^
Vì AC // DI ( cùng vuông góc với AB) mà DK ⊥ AC
=> DK ⊥ DI
hay ˆADKADK^ + ˆADIADI^ = 900
Do đó 1212ˆADCADC^ + 1212 ˆADBADB^ = 900
=> ˆADCADC^ + ˆADBADB^ = 1800
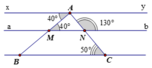


a) Vì x A M ^ = A M N ^ = 40 0 , mà hai góc này ở vị trí so le trong nên xy // MN (1)
Gọi đường thẳng chứa đoạn MN là ab
Ta có:
A N b ^ + A N M ^ = 180 0 ⇒ 130 0 + A N M ^ = 180 0 ⇒ A N M ^ = 180 0 − 130 0 ⇒ A N M ^ = 50 0
Vì A N M ^ = A C B ^ = 50 0 , mà hai góc này ở vị trí đồng vị nên MN // BC (2)
Từ (1) và (2) suy ra xy // MN // BC
b) Vì xy // MN nên x A N ^ = A N b ^ = 130 0 (hai góc so le trong)
Tia AM nằm giữa hai tia Ax và AN nên x A M ^ + M A N ^ = x A N ^ = 130 0
⇒ M A N ^ = 130 0 − 40 0 = 90 0 hay B A C ^ = 90 0
Vì MN // BC nên A B C ^ = A M N ^ = 40 0 (hai góc đồng vị)