Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

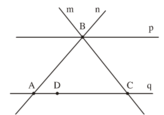
a, điểm A thuộc 2 đường thẳng n và q : A ∈ n, A ∈ q.
Điểm B thuộc ba đường thẳng m,n và p : B ∈ m, B ∈ n, B ∈ p.
b, Ba đường thẳng m,n, p đi qua điểm B: B ∈ m, B ∈ n , B ∈ p.
c, Điểm D nằm trên đường thẳng q và không nằm trên ba đường thẳng m,n,p: B ∈ q, B ∉ m, B ∉ n, B ∉ p.

Giải.
a, điểm A thuộc 2 đường thẳng n và q : A ∈ n, A ∈ q.
Điểm B thuộc ba đường thẳng m,n và p : B ∈ m, B ∈ n, B ∈ p.
b, Ba đường thẳng m,n, p đi qua điểm B: B ∈ m, B ∈ n , B ∈ p.
c, Điểm D nằm trên đường thẳng q và không nằm trên ba đường thẳng m,n,p: B ∈ q, B ∉ m, B ∉ n, B ∉ p.
Giải.
a, điểm A thuộc 2 đường thẳng n và q : A ∈ n, A ∈ q.
Điểm B thuộc ba đường thẳng m,n và p : B ∈ m, B ∈ n, B ∈ p.
b, Ba đường thẳng m,n, p đi qua điểm B: B ∈ m, B ∈ n , B ∈ p.
c, Điểm D nằm trên đường thẳng q và không nằm trên ba đường thẳng m,n,p: B ∈ q, B ∉ m, B ∉ n, B ∉ p.

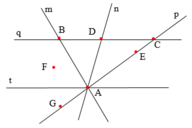
a) Điểm B thuộc đường thẳng m và đường thẳng q: ![]()
Điểm D thuộc đường thẳng n và đường thẳng q: ![]()
b) Bốn đường thẳng: p và q đi qua điểm C: ![]()
Hai đường thẳng: m, n, p và t đi qua điểm A: ![]()
c) Điểm E nằm trên đường thẳng p, điểm E không nằm trên các đường thẳng: m, n, q và t
d) Điêm F không thuộc đường thẳng nào.
e) Điểm B và D thuộc đường thẳng q mà không thuộc đường thẳng p
f) Các điểm: E, F, G, C không thuộc đường thẳng m, vừa không thuộc đường thẳng n

Ta có các số tự nhiên nhỏ hơn 10 và chia hết cho 3 là: 0; 3; 6; 9 nên Y = { 0; 3; 6; 9}
Do vậy 3 ∈∈ Y; 6 ∈∈ Y; 9 ∈∈ Y; 12 ∉∉Y.
3 thuộc Y vì 3<10 và chia hết cho 3.
6 thuộc Y vì 6<10 và chia hết cho 3.
9 thuộc Y vì 9<10 và chia hết cho 3.
12 không thuộc Y vì 12>10.


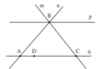
Điểm A thuộc các đường thẳng n, q. Kí hiệu A ∈ n; A ∈ q.
Điểm B thuộc các đường thẳng m, n, p. Kí hiệu B ∈ m; B ∈ n; B ∈ p.

Các đường thẳng đi qua điểm B là m, n, p. Kí hiệu B ∈ m; B ∈ n; B ∈ p.
Các đường thẳng đi qua điểm C là m , q. Kí hiệu C ∈ m , C ∈

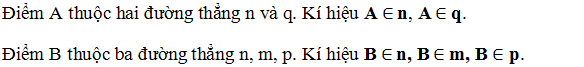

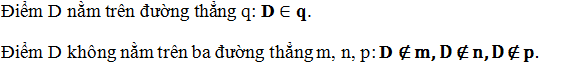

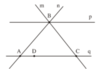
Điểm A thuộc các đường thẳng n, q. Kí hiệu A ∈ n; A ∈ q.
Điểm B thuộc các đường thẳng m, n, p. Kí hiệu B ∈ m; B ∈ n; B ∈ p.