Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
Chu kì dao động của vật không phụ thuộc vào biên độ nên nếu kích thích cho vật dao động với biên độ bằng 6 cm thì chu kì dao động của vật vẫn là T = 0,3 s
Chu kì dao động của động năng: T' = T 2 = 0 , 3 2 = 0 , 15 s

Chọn A
+ Chu kì dao động điều hòa của con lắc lò xo không phụ thuộc vào biên độ dao động.
+ T’ = T/2 = 0,15s.

Cách 1:
5 cm => 2s
=> 1 cm = 2 : 5 = 0,4 (s)
=> 10 cm = 0,4 . 10 = 4 (s)
Cách 2:
10 cm gấp 5 cm số lần là :
10 : 5 = 2 (lần)
Nếu kích thích con lắc 10 cm thì chu kì dao động là:
2 . 2 = 4 (s)

Khoảng thời gian vận tốc của vật không vượt quá \(6\pi cm/s\) là \(\frac{\Delta t}{T}=\frac{1}{3}\)
\(\Rightarrow\)Góc quét: \(\Delta\varphi=\frac{2\pi}{T}\frac{T}{3}=\frac{2\pi}{3}\left(rad\right)\)
\(\Rightarrow\) VTLG
-v
\(\Rightarrow\cos\varphi=\cos\left(90-30\right)=\frac{v}{v_{max}}=\frac{1}{2}\Rightarrow v_{max}=12\pi=\)\(\omega A\Rightarrow A=3,6cm\)

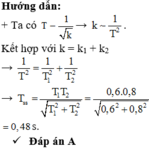
tỉ lệ T1/T2=4/3=> k1/k2= 9/16=> song song k=k1+k1=9/16+1=25/16=> T ss/T2=4/5=0,48s

Thời gian quả cầu đi từ vị trí cao nhất (x = -A) đến vị trí thấp nhất (x = A) chính là \(\frac{T}{2} = 0,2 => T = 0,4s.\)
Lực đàn hồi của lò xo khi lò xo ở vị trí thấp nhất chính là \(F_{dhmax} = k(A+\Delta l)\)
\(\frac{F_{max}}{P} = \frac{k(A+\Delta l)}{mg} = \frac{kA+k\Delta l }{mg } = 1+\frac{kA}{mg} =\frac{7}{4}\) (do \(k\Delta l = mg\))
=> \(A = \frac{3g}{4}\frac{m}{k} = \frac{3g}{4}.\frac{T^2}{4\pi^2} =0,03m = 3cm.\)
Chu kì dao động của vật chỉ phụ thuộc vào đặc tính của hệ nên luôn là 0,3 s.
Đáp án A