Bài 1 : Đặt một vật phẳng nhỏ vuông góc với trục chính của thấu kính hội tụ tiêu cự 20 cm cách kính 100 cm cho ảnh cao A1B1 . Di chuyển vật lại gần thấu kính một đoạn 40 cm thì thu được A2B2
a. Xác định chiều và khoảng dịch chuyển của A2B2
b. Tính tỉ số \(\frac{A_2B_2}{A_1B_1}\)
Bài 2 : Đặt vật sáng AB trên trục chính của một thấu kính hội tụ , cách kính 30 cm , thu được ảnh hiện...
Đọc tiếp
Bài 1 : Đặt một vật phẳng nhỏ vuông góc với trục chính của thấu kính hội tụ tiêu cự 20 cm cách kính 100 cm cho ảnh cao A1B1 . Di chuyển vật lại gần thấu kính một đoạn 40 cm thì thu được A2B2
a. Xác định chiều và khoảng dịch chuyển của A2B2
b. Tính tỉ số \(\frac{A_2B_2}{A_1B_1}\)
Bài 2 : Đặt vật sáng AB trên trục chính của một thấu kính hội tụ , cách kính 30 cm , thu được ảnh hiện rõ trên màn . Dịch chuyển vật lại gần thấu kính thêm 10 cm thì ta phải dịch chuyển màn ảnh thêm 1 đoạn nữa mới thu được ảnh rõ nét , ảnh sau cao gấp đôi ảnh trước
a. Hỏi phải dịch chuyển màn theo chiều nào ?
b. Tìm tiêu cự của thấu kính ?
Bài 3 : Một thấu kính hội tụ có tiêu cự 15 cm
a. Tính độ tụ của thấu kính
b. Một vật sáng AB đặt vuông góc với trục chính của thấu kính cho ảnh A'B' cách vật 60 cm . Xác định vị trí của vật và ảnh
c. Cố định thấu kính , dịch chuyển AB lại gần thấu kính thêm 10 cm . Xác định khoảng cách giữa vật và ảnh lúc này
Bài 4 : Một thấu kính hội tụ mỏng có tiêu cự f = 10 cm
a. Tính độ tụ của thấu kính
b. Vật sáng AB cao 2 cm đặt trên trục chính của thấu kính và vuông góc với trục chính (A thuộc trục chính ) , cách thấu kính 15 cm . Xác định vị trí , tính chất và độ cao ảnh A1B1 của vật AB qua thấu kính . Vẽ ảnh theo đúng tỉ lệ
c. Cố định thấu kính . Xác định vị trí đặt vật AB nói trên để ảnh qua thấu kính là ảnh ảo , cách vật 9 cm
d. Chứng tỏ khoảng cách giữa vật thật và ảnh thật qua thấu kính hội tụ có một giá trị cực tiểu . Tính giá trị cực tiểu đó đối với bài toán này .





![]()
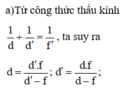
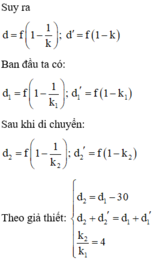
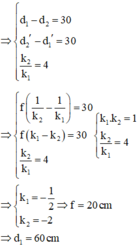
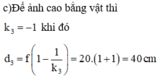

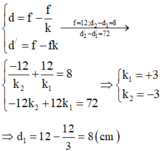


Chọn đáp án A
+ Khi chưa dịch vật ta có: 1 d + 1 d ' = 1 f = 1 12
+ Khi đó ảnh là ảnh ảo nên d ' < 0 và nằm trước thấu kính => Sau khi dịch vật thì cho ảnh thật => nằm sau thấu kính và cách thấu kính một đoạn bằng 72 + d ' d o d ' < 0
Vậy ta có: 1 d + 8 + 1 d ' + 72 = 1 f = 1 12
Kết hợp hai phương trình trên giải hệ ta thu được:
d ' = d f d − f = 12 d d − 12 ⇒ 1 d + 8 + 1 12 d d − 12 = 1 12 ⇒ d = 8 c m