Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Phương pháp:
sử dụng điều kiện vân sáng, điều kiện chồng chập vân
Cách giải:
Điều kiện để 1 vị trí có hai quang phổ bậc k và bậc k+1 chồng chập lên nhau là :

Vì k nguyên nên chọn k =2. Hiện tượng chồng chập diễn ra khi k = 2 và 3.
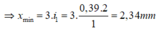
Đáp án B

Tóm tắt:
a = \(10^{-3}m\)
D = \(1,25m\)
\(\lambda_1=0,64\mu m\)
\(\lambda_2=0,48\mu m\)
\(\Delta x=?\)
Giải:
Khi vân sáng trùng nhau:
\(k_1\lambda_1=k_2\lambda_2\Rightarrow\)\(\frac{k_1}{k_2}=\frac{\lambda_2}{\lambda_1}=\frac{0,48}{0,64}=\frac{3}{4}\)
Vậy: \(k_1=3;k_2=4\)\(\Rightarrow\Delta x=3i_1=3.\frac{\lambda_1.D}{a}=3.\)\(\frac{0,64.10^{-6}.1,25}{10^{-3}}=2,4.10^{-3}m=2,4mm\)
\(\rightarrow D\)

Tại điểm M là vân sáng nên \(x_M=ki=k\frac{\lambda D}{a}\)
\(\lambda=\frac{x_Ma}{kD}=\frac{4,2.0,5}{k.1,4}=\frac{1,5}{k}\)
Theo giả thiết: \(0,38\le\lambda\le0,76\)
\(\Rightarrow0,38\le\frac{1,5}{k}\le0,76\)
\(\Rightarrow1,97\le k\le3,94\)
k nguyên nên k = 2,3.
Như vậy, tại M có 2 bước sóng cho vân sáng, đáp án là A.

Tịnh tiến màn quan sát lại gần mặt phẳng chưa hai khe 25 cm tức là \(D' = D-0,25.\)
\(i_1 = \frac{\lambda D}{a}\\
i_2 =\frac{\lambda (D-0,25)}{a} \)=> \(\frac{i}{i'}= \frac{D}{D-0,25}= \frac{5}{4}\)
=> \(D = 5.0,25 = 1,25m.\)
=> \(\lambda = \frac{i.a}{D}= 0,48 \mu m.\)
Chú ý là giữ nguyên đơn vị i (mm); a (mm) ; D (m) thì đơn vị bước sóng \(\lambda (\mu m)\).

- Điều kiện để cho vân sáng tại vị trí M của bức xạ đơn sắc:
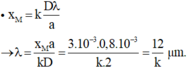
- Với khoảng giá trị của bước sóng 0,38 µm ≤ λ ≤0,76 µm. Sử dụng chức năng Mode → 7 ta tìm được tại M có hai bức xạ đơn sắc cho vân sáng ứng với:
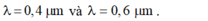

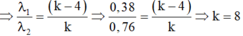
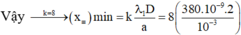
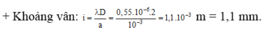
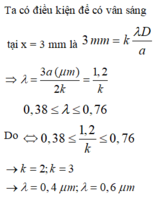

Đáp án B
Điều kiện để 1 vị trí có hai quang phổ bậc k và bậc k+1 chồng chập lên nhau là :
Vì k nguyên nên chọn k =2. Hiện tượng chồng chập diễn ra khi k = 2 và 3.