Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Màu sắc của vân trung tâm được tạo thành do sự chồng chập của ba ánh sáng đơn sắc λ 1 , λ 2 , λ 3
Vậy toạ độ những vân sáng cùng màu vân trung tâm thoả mãn
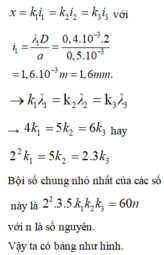

Vậy ta thấy giá trị khả dĩ lớn nhất của n bằng 4.
Vậy tổng số vân cùng màu vân trung tâm là N = 1 + 2.4 = 9 vân.
Đáp án C

Chọn C
Ta có: i = λD/a = 2mm.
Số vân sáng trên màn là:
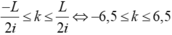
=> Có 13 giá trị của k thỏa mãn
Vậy trên màn có 13 vân sáng

\(i = \frac{\lambda D}{a}=\frac{0,5.2}{0,5}= 2mm.\)
Số vân sáng trên màn quan sát là
\(N_s= 2.[\frac{L}{2i}]+1 =2.6+1 = 13.\)

Khoảng vân: \(i=\dfrac{\lambda D}{a}=\dfrac{0,5\cdot10^{-6}\cdot2}{2\cdot10^{\cdot3}}=5\cdot10^{-4}m=0,5mm\)
Khoảng cách từ vân sáng bậc 2 đến vân sáng bậc 4 cùng phía so với vân trung tâm cách nhau là:
\(\Delta i=4i-2i=2i=2\cdot0,5=1mm\)

Tọa độ vân sáng: x = kλD/a →λ= ax/kD = 2,7/k μm
Vì 0,4 μm ≤ λ ≤ 0,76 μm nên 3,6 ≤ k ≤ 6,75
Suy ra: k = 4, 5, 6 ; tương ứng với λ = 0,450 μm ; 0,540 μm và 0,675 μm.
Chọn đáp án D

Chọn A
Ta có: 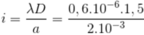 = 0,45mm.
= 0,45mm.
Số vân sáng trong đoạn MN là:
OM/i < k < ON/i=> 11,1< k < 22,2
=> Có 11 giá trị của k thỏa mãn.
Vậy có 11 vân sáng.

Phương pháp:
Khoảng vân i = λD/a là khoảng cách giữa hai vân sáng hoặc hai vân tối liên tiếp.
Cách giải:
Khoảng vân:
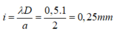
Khoảng cách giữa vân sáng bậc 3 và vân sáng bậc 5 ở hai bên vân trung tâm là: d = 3i + 5i = 8i = 2 mm
Chọn B

Chọn C
Ta có i=1,1 mm.
L/2i = 7,7 =>
Trên màn có 15 vân sáng và 16 vân tối.

Cách giải:
Giải: Trên đoạn MN có 6 vân sáng => khoảng vân i = 12/(6 – 1) = 2,4 mm. Bước sóng λ = i.a/D = 2,4.0,5/2 = 0,6 μm => Chọn B