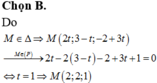
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
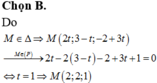
\(\frac{\frac{1}{4}+\frac{1}{24}+\frac{1}{124}}{\frac{3}{4}+\frac{3}{24}+\frac{3}{124}}\) + \(\frac{\frac{2}{7}+\frac{2}{17}+\frac{2}{127}}{\frac{3}{7}+\frac{3}{17}+\frac{3}{127}}\)
= \(\frac{\frac{1}{4}+\frac{1}{24}+\frac{1}{124}}{3.\left(\frac{1}{4}+\frac{1}{24}+\frac{1}{124}\right)}\) + \(\frac{2.\left(\frac{1}{7}+\frac{1}{17}+\frac{1}{127}\right)}{3.\left(\frac{1}{7}+\frac{1}{17}+\frac{1}{127}\right)}\)
= \(\frac{1}{3}\) + \(\frac{2}{3}\) = 1
Ta có :
\(\frac{1}{1^2}< \frac{1}{1.2};\frac{1}{2^2}< \frac{1}{2.3};...;\frac{1}{50^2}< \frac{1}{49.50}\)
\(\Leftrightarrow\frac{1}{1^2}+\frac{1}{2^2}+\frac{1}{3^2}+...+\frac{1}{50^2}< \frac{1}{1.2}+\frac{1}{2.3}+...+\frac{1}{49.50}=1-\frac{1}{50}< 1< 2\)
Vậy A < 2
\(\frac{1}{1^2}=1\)
\(\frac{1}{2^2}< \frac{1}{1.2}\)
\(\frac{1}{3^2}< \frac{1}{2.3}\)
\(...\)
\(\frac{1}{50^2}< \frac{1}{49.50}\)
\(\Rightarrow\frac{1}{1^2}+\frac{1}{2^2}+\frac{1}{3^2}+...+\frac{1}{50^2}< 1+\frac{1}{1.2}+\frac{1}{2.3}+...+\frac{1}{49.50}\)
\(\Rightarrow A< 1+1-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+...+\frac{1}{49}-\frac{1}{50}\)
\(\Rightarrow A< 1+1-\frac{1}{50}\)
\(\Rightarrow A< 2-\frac{1}{50}< 2\)
Vậy \(A< 2\)
Câu 1:
Đa thức \(f\left(x\right)=x^2-5x\) nhận 0 và 5 làm nghiệm vì f(0)=f(5)=0
Câu 2:
\(g\left(1\right)=1-6+5=0\)
nên x=1 là nghiệm của đa thức g(x)
Em mong mọi người giúp em với ạ.
