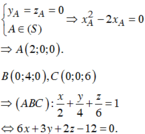Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
Ta có các điểm A,B,C có tọa độ lần lượt như sau A(−2;0;0), B(0;3;0), C(0;0;4).
Phương trình mặt phẳng (ABC) theo đoạn chắn là x − 2 + y 3 + z 4 = 1 .
Phương trình tổng quát của mặt phẳng (ABC) là − 6 x + 4 y + 3 z − 12 = 0 .

Đáp án C
Ta có: A(-3;0;0), B(0;2;0), C(0;0;4)
Suy ra A B C : x - 3 + y 2 + z 4 = 1 hay 4x - 6y - 3z + 12 = 0
Do vậy mặt phẳng 4x - 6y - 3z + 12 = 0 song song với mặt phẳng (ABC)

Đáp án C.
Phương pháp:
Mặt phẳng P : A x + B y + C z + D = 0 có 1 VTPT là n → = A ; B ; C .
Cách giải:
P : x − 4 y + 3 z − 2 = 0 có một vecto pháp tuyến là n 3 → = − 1 ; 4 ; − 3 .

Đáp án A.
6 x - 3 y + 2 z - 12 = 0 .
Tương tự
B 0 ; 4 ; 0 , C 0 ; 0 ; 6 ⇒ A B C : x 2 + y 4 + z 6 = 1 ⇔ 6 x + 3 y + 2 z − 12 = 0.

Đáp án C.
Gọi I x ; y ; z thỏa mãn
I A → + 2 I B → + 5 I C → = 0 ⇒ x = 3 + 2. ( − 3 ) + 5. ( − 1 ) 8 = − 1 y = − 1 + 2.0 + 5. ( − 3 ) 8 = − 2 z = − 3 + 2. ( − 1 ) + 5.1 8 = 0
⇒ I = ( − 1 ; − 2 ; 0 )
Ta có
M A → + 2 M B → + 5 M C → = M I → + I A → + 2 M I → + 2 I B → + 5 M I → + 5 I C →
= 8 M I → + I A → + 2 I B → + 5 I C → = 8 M I →
⇒ M A → + 2 M B → + 5 M C → min ⇔ 8 M I → min <=> M là hình chiếu của I lên (P)
Gọi Δ là đường thẳng đi qua I − 1 ; 2 ; 0 và vuông góc với
( P ) : 2 x + 4 y + 3 z − 19 = 0 có vectơ chỉ phương là 2 ; 4 ; 3 ⇒ Δ : x = − 1 + 2 t y = − 2 + 4 t z = 3 t
Thế vào (P)
⇒ 2 ( − 1 + 2 t ) + 4 ( − 2 + 4 t ) + 3 ( 3 t ) − 19 ⇔ t = 1
⇒ x = 1 y = 2 z = 3 ⇒ M 1 ; 2 ; 3 ⇒ a + b + c = 6