Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
Phương pháp : Nếu n → là 1VTPT của (P) => k n → (k≠0) cũng là 1 VTPT của (P)

vì (C) đi qua điểm A nên tọa độ điểm A thỏa mãn pt \(y=\frac{ax^2-bx}{x-1}\) ta có \(\frac{5}{2}=\frac{a+b}{-2}\Rightarrow a+b=-5\)
vì tiếp tuyến của đồ thị tại điểm O có hệ số góc =-3 suy ra y'(O)=-3
ta có \(y'=\frac{ax^2-2ax+b}{\left(x-1\right)^2}\) ta có y'(O)=b=-3 suy ra a=-2
vậy ta tìm đc a và b

Đáp án C
Phương pháp giải:
Vectơ pháp tuyến của mặt phẳng chính là tọa độ vectơ tích có hướng
Lời giải:
Ta có A B → = 2 ; 2 ; − 1 ; A C → = − 1 ; − 1 ; 0 suy ra A B → ; A C → = − 1 ; 1 ; 0

Đáp án C.
Mặt phẳng ( P ) : y − z + 2 = 0 có một vecto7 pháp tuyến là n → = ( 0 ; 1 ; − 1 )

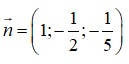
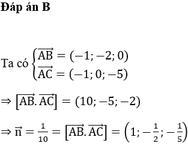


Mặt phẳng (ABC) cắt các trục tọa độ Ox, Oy, Oz lần lượt tại A(1;0;;0), B(0;1;0),C(0;0-2)
⇒ ( A B C ) : x 1 + y 1 + z - 2 = 1 ⇔ 2 x + 2 y - z + 2 = 0
⇒ ( A B C ) nhận vectơ n ⇀ = ( 2 ; 2 ; - 1 ) làm VTPT.
Chọn đáp án A.