Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Đáp án A
Vì mặt phẳng (P) đi qua A, B nên
3 a - 2 b + 6 c - 2 = 0 b = 2 ⇔ a = 2 - 2 c b = 2 ⇒ ( P ) : ( 2 - 2 c ) x + 2 y + c z = 0
Khoảng cách từ tâm I (1;2;3) của (S) đến (P) là:
d(I,(P))= ( 2 - 2 c ) + 2 . 2 + c . 3 - 2 ( 2 - 2 c ) 2 + 2 2 + c 2 = c + 4 5 c 2 - 8 c + 8
Khi đó bán kính của đường tròn giao tuyến là:
r= 25 - ( c + 4 ) 2 5 c 2 - 8 c + 8 = 124 c 2 - 208 c + 184 5 c 2 - 8 c + 8
Để r đạt giá trị nhỏ nhất thì hàm số
f(t)= 124 t 2 - 208 t + 184 5 t 2 - 8 t + 8 trên [1;+ ∞ ) phải nhỏ nhất
Ta có: f'(t)= 48 t 2 + 144 t - 192 ( 5 t 2 - 8 t + 8 ) 2 ,
f'(t)=0
⇔
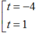
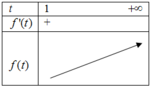
Khi đó hàm số đạt giá trị nhỏ nhất tại t=1 ⇒ c=1
Ta có: T=a+b+c=2-2c+2=4-c=3
Đáp án B
Phương pháp:
- Đưa phương trình mặt phẳng (P) về dạng chỉ còn 1 tham số.
- (P) cắt (S) theo giao tuyến là đường tròn có bán kính nhỏ nhất <=> d(I;(P)) max, trong đó: I là tâm mặt cầu (S).
Cách giải:
( S ) : x - 1 2 + y - 2 2 + z - 3 2 = 25 có tâm I(1;2;3) và bán kính R = 5
- (P) cắt (S) theo giao tuyến là đường tròn có bán kính nhỏ nhất <=> d(I;(P)) max, trong đó: I là tâm mặt cầu (S)
Ta có
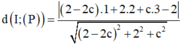
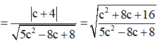
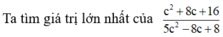
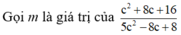
Ta có:
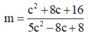
(*) có nghiệm
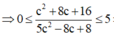
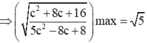
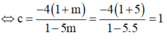
Khi đó T =a+b+c =2-2c+2+c=4-1 =3
Đáp án A
Phương pháp:
+) Để mặt phẳng (P) cắt (S) theo giao tuyến là đường tròn có bán kính nhỏ nhất thì d ( I ; ( P ) ) m a x
+) Gọi H và K lần lượt là chân đường vuông góc của I trên (P) và trên đường thẳng AB. Ta có: HI ≤ IK
Cách giải:
Khi đó mặt phẳng (P) có dạng :
Mặt cầu (S) có tâm I(1;2;3), bán kính R = 5
Gọi H và K lần lượt là chân đường vuông góc của I trên (P) và trên đường thẳng AB. Ta có : HI ≤ IK
Để mặt phẳng (P) cắt (S) theo giao tuyến là đường tròn có bán kính nhỏ nhất thì
=>Phương trình đường thẳng AB:
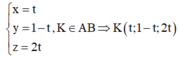
Vì
là 1 VTPT của (P)
=> I H → và vec tơ pháp tuyến n ( P ) → = ( 2 - 2 c ; 2 ; c ) cùng phương
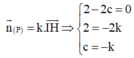
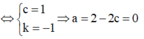
19.
Phương trình mặt phẳng theo đoạn chắn:
\(\frac{x}{3}+\frac{y}{-4}+\frac{z}{-2}=1\)
\(\Leftrightarrow4x-3y-6z-12=0\)
20.
Phương trình mặt phẳng (ABC) theo đoạn chắn:
\(\frac{x}{1}+\frac{y}{2}+\frac{z}{3}=1\)
\(\Leftrightarrow6x+3y+2z-6=0\)
Chẳng đáp án nào đúng cả, chắc bạn ghi nhầm đáp án C số 1 thành số 0 :)
15.
\(2\left(x-2\right)-5\left(y+3\right)+1\left(z+2\right)=0\)
16.
\(\overrightarrow{n_1}=\left(1;1;-1\right)\) ; \(\overrightarrow{n_2}=\left(1;-1;1\right)\)
\(\left[\overrightarrow{n_1};\overrightarrow{n_2}\right]=\left(0;-2;-2\right)=-2\left(0;1;1\right)\)
Phương trình (P):
\(1\left(y-1\right)+1\left(z-1\right)=0\Leftrightarrow y+z-2=0\)
17.
\(\overrightarrow{n_P}=\left(1;-1;1\right)\) ; \(\overrightarrow{n_Q}=\left(3;2;-12\right)\)
\(\left[\overrightarrow{n_P};\overrightarrow{n_Q}\right]=\left(10;15;5\right)=5\left(2;3;1\right)\)
Phương trình mặt phẳng (R):
\(2x+3y+z=0\)
18.
\(\overrightarrow{MN}=\left(0;-2;3\right);\overrightarrow{MP}=\left(-2;1;3\right)\)
\(\left[\overrightarrow{MN};\overrightarrow{MP}\right]=\left(-9;-6;-4\right)=-1\left(9;6;4\right)\)
Phương trình:
\(9\left(x-2\right)+6\left(y-2\right)+4z=0\)
\(\Leftrightarrow9x+6y+4z-30=0\)
16.
\(\overrightarrow{n_{\left(P\right)}}=\left(2;1;-1\right)\) ; \(\overrightarrow{n_{\left(Q\right)}}=\left(1;-2;1\right)\)
\(\left[\overrightarrow{n_{\left(P\right)}};\overrightarrow{n_{\left(Q\right)}}\right]=\left(-1;-3;-5\right)\)
\(\Rightarrow\) Giao tuyến 2 mp nhận \(\left(-1;-3;-5\right)\) hoặc \(\left(1;3;5\right)\) là 1 vtcp
17.
Đường thẳng nhận \(\left(2;-3;6\right)\) là 1 vtcp
Pt tham số: \(\left\{{}\begin{matrix}x=-2+2t\\y=4-3t\\z=3+6t\end{matrix}\right.\)
Pt chính tắc: \(\frac{x+2}{2}=\frac{y-4}{-3}=\frac{z-3}{6}\)
18.
Pt tham số đường thẳng d qua A và vuông góc (P): \(\left\{{}\begin{matrix}x=-2+t\\y=1+t\\z=5-t\end{matrix}\right.\)
H là giao điểm d và (P) nên tọa độ thỏa mãn:
\(-2+t+1+t-5+t+9=0\Rightarrow t=-1\) \(\Rightarrow H\left(-3;0;6\right)\)
19.
Pt mặt phẳng (P) qua A và vuông góc d:
\(3\left(x-4\right)+2\left(y+3\right)-z=0\)
\(\Leftrightarrow3x+2y-z-6=0\)
Pt d dạng tham số: \(\left\{{}\begin{matrix}x=-2+3t\\y=-2+2t\\z=-t\end{matrix}\right.\)
H là giao điểm d và (P) nên tọa độ thỏa mãn:
\(3\left(-2+3t\right)+2\left(-2+2t\right)+t=0\Rightarrow t=\frac{5}{7}\) \(\Rightarrow H\left(\frac{1}{7};-\frac{4}{7};-\frac{5}{7}\right)\)
14.
\(\overrightarrow{BA}=\left(4;2;0\right)=2\left(2;1;0\right)\)
Gọi M là trung điểm AB \(\Rightarrow M\left(-1;1;-1\right)\)
Mp trung trực AB vuông góc AB và qua M có pt:
\(2\left(x+1\right)+1\left(y-1\right)=0\Leftrightarrow2x+y+1=0\)
15.
Gọi pt \(\left(Q\right)\) có dạng \(ax+by+cz+d=0\) (\(d\ne0\))
(Q) qua A nên: \(2a+d=0\) \(\Rightarrow d=-2a\)
\(\left(P\right)\perp\left(Q\right)\Leftrightarrow2b-c=0\) \(\Rightarrow c=2b\)
\(d\left(O;\left(Q\right)\right)=\frac{4}{3}\Leftrightarrow\frac{\left|d\right|}{\sqrt{a^2+b^2+c^2}}=\frac{4}{3}\Leftrightarrow9d^2=16\left(a^2+b^2+c^2\right)\) \(\Leftrightarrow36a^2=16\left(a^2+b^2+4b^2\right)\) \(\Leftrightarrow20a^2=80b^2\Leftrightarrow\left[{}\begin{matrix}a=2b\\a=-2b\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}a=2;b=1;c=2;d=-4\\a=2;b=-1;c=-2;d=-4\end{matrix}\right.\) Có 2 mặt phẳng (Q) thỏa mãn: \(\left[{}\begin{matrix}2x+y+2z-4=0\\2x-y-2z-4=0\end{matrix}\right.\)
Mặt cầu (S) có tâm I(3, -2, 1) và bán kính R = 10.
Khoảng cách từ tâm I của mặt cầu (S) đến mặt phẳng (α) là:
d(I, α) = ∣∣ ∣∣2.3−2.(−2)−1+9√22+(−2)2+(−1)2∣∣ ∣∣=183=6|2.3−2.(−2)−1+922+(−2)2+(−1)2|=183=6
Vì d(I, α) < R ⇒⇒ Mặt phẳng (α) cắt mặt cầu (S) theo đường tròn (C) có phương trình (C):
{2x−2y−z+9=0(x−3)2+(y+2)2+(z−1)2=100{2x−2y−z+9=0(x−3)2+(y+2)2+(z−1)2=100
Tâm K của đường tròn (C) là hình chiếu vuông góc của tâm I của mặt cầu trên mặt phẳng (α).
Mặt phẳng (α) có vectơ pháp tuyến →nn→ = (2, -2. -1).
Đường thẳng d qua I và vuông góc với (α) nhận →nn→ = (2, -2, -1) làm vectơ chỉ phương và có phương trình d :
⎧⎪⎨⎪⎩x=3+2ty=−2−2tz=1−t{x=3+2ty=−2−2tz=1−t
Thay t = -2 vào phương trình của d, ta được toạ độ tâm K của đường tròn (C).
⎧⎪⎨⎪⎩x=3+2.(−2)=−1y=−2−2.(−2)=2z=1−2.(−2)=3{x=3+2.(−2)=−1y=−2−2.(−2)=2z=1−2.(−2)=3
⇒⇒ K(-1, 2, 3)
Ta có: IK2 = (-1 - 3)2 + (2 + 2)2 + (3 - 1)2 = 36.
Bán kính r của đường tròn (C) là:
r2 = R2 - IK2 = 102 - 36 = 64 ⇒⇒ r= 8
Giải
Mặt cầu (S) có tâm I(3, -2, 1) và bán kính R = 10.
Khoảng cách từ tâm I của mặt cầu (S) đến mặt phẳng (α) là:
d(I, α) = ∣∣ ∣∣2.3−2.(−2)−1+9√22+(−2)2+(−1)2∣∣ ∣∣=183=6|2.3−2.(−2)−1+922+(−2)2+(−1)2|=183=6
Vì d(I, α) < R ⇒⇒ Mặt phẳng (α) cắt mặt cầu (S) theo đường tròn (C) có phương trình (C):
{2x−2y−z+9=0(x−3)2+(y+2)2+(z−1)2=100{2x−2y−z+9=0(x−3)2+(y+2)2+(z−1)2=100
Tâm K của đường tròn (C) là hình chiếu vuông góc của tâm I của mặt cầu trên mặt phẳng (α).
Mặt phẳng (α) có vectơ pháp tuyến →nn→ = (2, -2. -1).
Đường thẳng d qua I và vuông góc với (α) nhận →nn→ = (2, -2, -1) làm vectơ chỉ phương và có phương trình d :
⎧⎪⎨⎪⎩x=3+2ty=−2−2tz=1−t{x=3+2ty=−2−2tz=1−t
Thay t = -2 vào phương trình của d, ta được toạ độ tâm K của đường tròn (C).
⎧⎪⎨⎪⎩x=3+2.(−2)=−1y=−2−2.(−2)=2z=1−2.(−2)=3{x=3+2.(−2)=−1y=−2−2.(−2)=2z=1−2.(−2)=3
⇒⇒ K(-1, 2, 3)
Ta có: IK2 = (-1 - 3)2 + (2 + 2)2 + (3 - 1)2 = 36.
Bán kính r của đường tròn (C) là:
r2 = R2 - IK2 = 102 - 36 = 64 ⇒⇒ r= 8
Chọn C
* Ta có: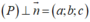
trong đó a;b;c không đồng thời bằng 0. Mặt cầu (S) có tâm I (1;2;3) và bán kính R=5.
Do mặt phẳng (P) chứa đường thẳng AB nên ta có:
* Bán kính đường tròn giao tuyến là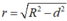
trong đó
Để bán kính đường tròn nhỏ nhất điều kiện là d lớn nhất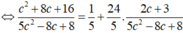
lớn nhất 
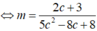lớn nhất.
Coi hàm số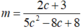
là một phương trình ẩn c ta được
5mc²-2 (4m+1)c+ (8m-3)=0,
phương trình có nghiệm c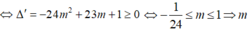
lớn nhất
<=> c = 1 => a = 0 => M = 2a + b – c = 1