Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Kiểm tra thấy A và B nằm khác phía so với mặt phẳng (P)
Ta tìm được điểm đối xứng với B qua (P) là B ' ( -1;-3;4 )
Lại có M A - M B = M A - M B ' ≤ A B ' = c o n s t .
Vậy M A - M B đạt giá trị lớn nhất khi M, A, B’ thẳng hàng hay M là giao điểm của đường thẳng AB’ với mặt phẳng (P).
Đường thẳng AB’ có phương trình tham số là x = 1 + t y = - 3 z = - 2 y .
Tọa độ điểm M ứng với tham số t là nghiệm của phương trình
1 + t + - 3 + - 2 t - 1 = 0 ⇔ t = - 3 ⇒ M - 2 ; - 3 ; 6
Suy ra a = -2; b = -3; c = 6
Vậy a + b + c = 1
Đáp án A

Lời giải:
\(A=a_1a_2+a_2a_3+....+a_{n-1}a_n+a_na_1=0\)
Nếu $n$ lẻ, ta thấy tổng $A$ gồm lẻ số hạng, mỗi số hạng có giá trị $1$ hoặc $-1$ nên $A$ lẻ \(\Rightarrow A\neq 0\) (vô lý)
Do đó $n$ chẵn. Nếu $n$ có dạng $4k+2$. Vì $A=0$ nên trong $4k+2$ số hạng trên sẽ có $2k+1$ số có giá trị là $1$ và $2k+1$ số có giá trị $-1$. Vì mỗi số $a_i$ trong $A$ xuất hiện $2$ lần nên \(a_1a_2a_2a_3....a_{n-1}a_na_{n}a_{1}=(a_1a_2...a_n)^2=1^{2k+1}(-1)^{2k+1}=-1\) (vô lý)
Do đó $n$ phải có dạng $4k$, tức là $n$ chia hết cho $4$ (đpcm)

Áp dụng BĐT tam giác ta có:
a+b>c =>c-a<b =>c2-2ac+a2<b2
a+c>b =>b-c <a =>b2-2bc+c2<a2
b+c>a =>a-b<c =>a2-2ab+b2<c2
Suy ra: c2-2ac+a2+b2-2bc+c2+a2-2ab+b2<a2+b2+c2
<=>-2.(ab+bc+ca)+2.(a2+b2+c2)<a2+b2+c2
<=>-2(ab+bc+ca)<-(a2+b2+c2)
<=>2.(ab+bc+ca)<a2+b2+c2
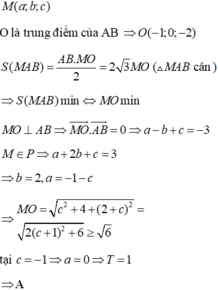

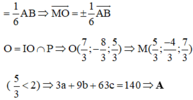

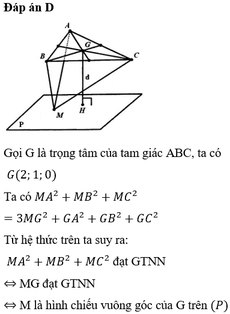




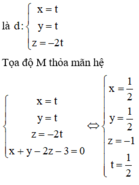
Gọi I là trung điểm A B ⇒ I 5 2 ; 0 ; 5 2 ; AB = 5
M thuộc mặt cầu x - 5 2 2 + y 2 + z - 5 2 2 = 25 4
Tọa độ điểm M là nghiệm của hệ
z = 0 x - 5 2 2 + y 2 + z - 5 2 2 = 25 4
Hạ M H ⊥ A B ; H K ⊥ O x y A B ∥ O x y ⇒ H K = d A B , O x y không đổi mà M H ≥ H K nên S ∆ A B M nhỏ nhất ⇔ MH nhỏ nhất ⇔ M nằm trên đường thẳng ∆ là hình chiếu vuông góc của AB lên mặt phẳng ( Oxy ). Mặt khác (S) tiếp xúc với mặt phẳng ( Oxys ) nên M ∈ ∆
Vậy M 5 2 ; 0 ; 0
Đáp án A