Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lần sau em đăng trong h.vn
1. \(log_{ab}c=\frac{1}{log_cab}=\frac{1}{log_ca+log_cb}=\frac{1}{\frac{1}{log_ac}+\frac{1}{log_bc}}=\frac{1}{\frac{log_ac+log_bc}{log_ac.log_bc}}=\frac{log_ac.log_bc}{log_ac+log_bc}\)
Đáp án B:
2. \(f'\left(x\right)=-4x^3+8x\)
\(f'\left(x\right)=0\Leftrightarrow-4x^3+8x=0\Leftrightarrow x=0,x=\sqrt{2},x=-\sqrt{2}\)
Có BBT:
x -căn2 0 căn2 f' f 0 0 0 - + - +
Nhìn vào bảng biên thiên ta có hàm số ... là đáp án C

Đáp án: B.
Xét f(x) = x 3 + m x 2 + x - 5
Vì 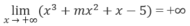
và f(0) = -5 với mọi m ∈ R cho nên phương trình f(x) = 0 luôn có nghiệm dương.

Đáp án: B.
Xét f(x) = x 3 + m x 2 + x - 5
Vì 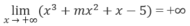
và f(0) = -5 với mọi m ∈ R cho nên phương trình f(x) = 0 luôn có nghiệm dương.

a) Hàm có cực đại, cực tiểu khi mà $y'=-3x^2+2(m-1)x=x[2(m-1)-3x]$ có ít nhất hai nghiệm phân biệt $\Leftrightarrow 2(m-1)-3x=0$ có một nghiệm khác $0$ hay $m\neq 1$
b) Đồ thị hàm số $(\star)$ cắt trục hoành tại ba điểm phân biệt khi mà phương trình $y=-x^3+(m-1)x^2-m+2=0$ có $3$ nghiệm phân biệt
$\Leftrightarrow (1-x)[x^2+x(2-m)+(2-m)]=0$ có ba nghiệm phân biệt
$\Leftrightarrow x^2+x(2-m)+(2-m)=0$ có hai nghiệm phân biệt khác $1$
Do đó ta cần có $\left\{\begin{matrix}1+2-m+2-m=5-2m\neq 0\\ \Delta =(2-m)^2-4(2-m)>0\end{matrix}\right.$
Vậy để thỏa mãn đề bài thì $m\neq \frac{5}{2}$ và $m>2$ hoặc $m<-2$
c) Gọi điểm cố định mà đồ thị hàm số đi qua là $(x_0,y_0)$
$y_0=-x_0^3+(m-1)x_0^2-m+2$ $\forall m\in\mathbb{R}$
$\Leftrightarrow m(x_0^2-1)-(x_0^3+x_0^2+y_0-2)=0$ $\forall m\in\mathbb{R}$
$\Rightarrow\left{\begin{matrix}x_0^2=1\\ x_0^3+x_0^2+y_02=0\end{matrix}\right.\begin{bmatrix}(x_0,y_0)=(1;0)\\ (x_0,y_0)=(-1;2)\end{bmatrix}$
Viết lại đoạn cuối:
$\Rightarrow\left{\begin{matrix}x_0^2=1\\x_0^3+x_0^2+y_0-2=0\end{matrix}\right.$ $\Rightarrow \begin{bmatrix}(x_0,y_0)=(1;0)\\ (x_0,y_0)=(-1;2)\end{bmatrix}$



nên từ đồ thị (C) ta suy ra ngay đồ thị của hàm số :
\(y=\left|\dfrac{x^3}{6}+\dfrac{3x^2}{2}+\dfrac{5x}{2}\right|\) là hình 18


a) y′=3x+2(m+3)x=x[3x+2(m+3)];y′=0⇔x1=0y′=3x2+2(m+3)x=x[3x+2(m+3)];y′=0⇔x1=0
hoặc x2=−2m+63x2=−2m+63
Xảy ra hai trường hợp đối với dấu của y':
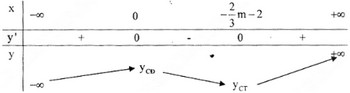
Rõ ràng, để hàm số có điểm cực đại tại x = -1 ta phải có
x2=−2m+63=−1⇔m=−32x2=−2m+63=−1⇔m=−32
(Chú ý : trường hợp x1 = x2 thì hàm số không có cực trị).
b) (Cm) cắt Ox tại x = -2 ⇔ -8 + 4(m + 3) + 1 - m = 0 ⇔ m=−53m=−53
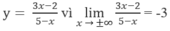
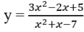
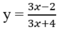 luôn nghịch biến;
luôn nghịch biến;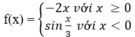

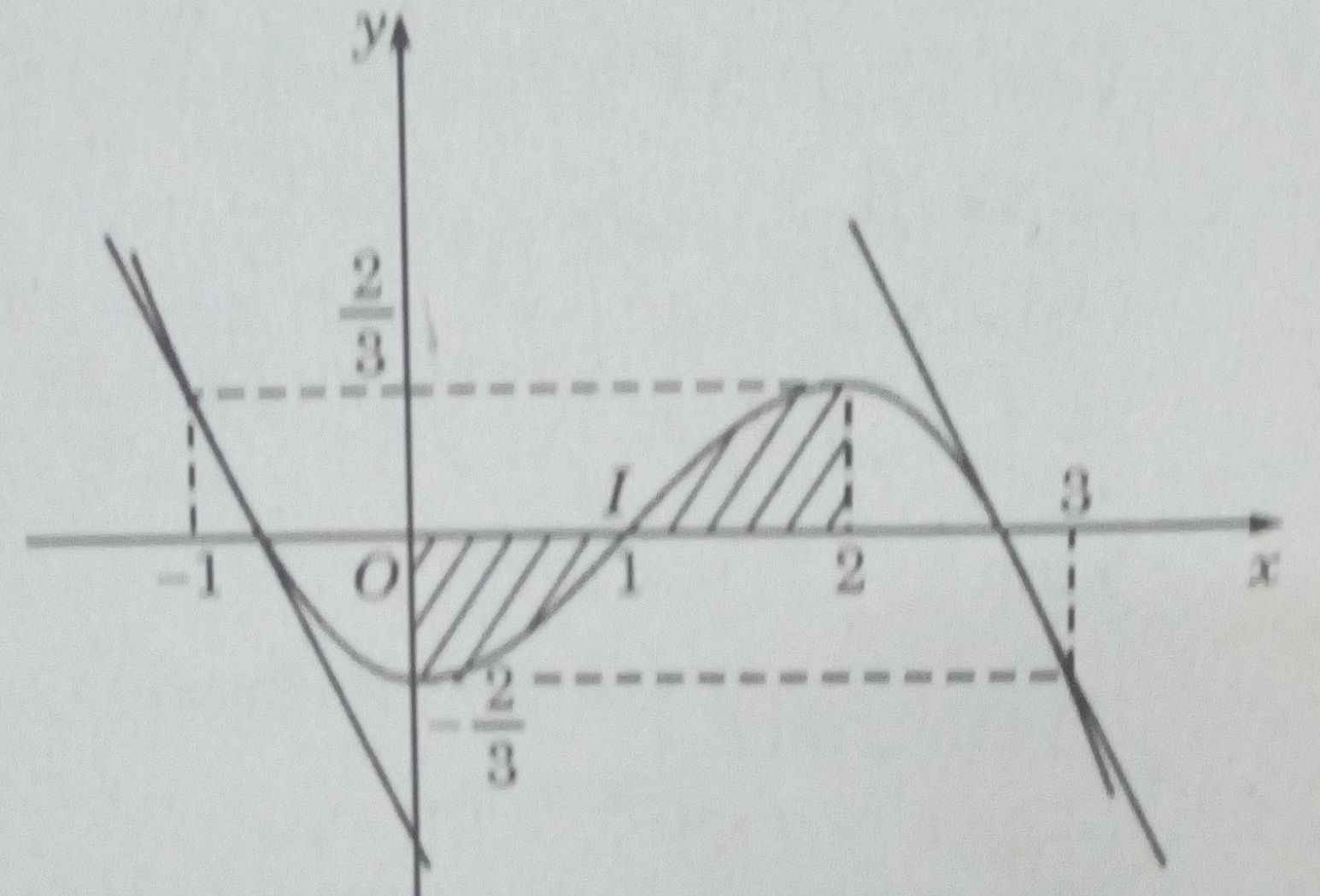

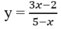 là y = -3;
là y = -3;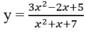
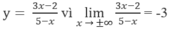
Chọn A