K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
SG
1

KD
25 tháng 4 2017

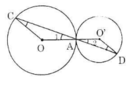
Tam giác COA cân: ∠C = ∠A1
Tam giác DO’A cân: ∠D = ∠A2
Mà ∠A1 = ∠A2 (đối đỉnh)
⇒ ∠C = ∠D ⇒ OC//O’D
PT
1

CM
3 tháng 8 2018
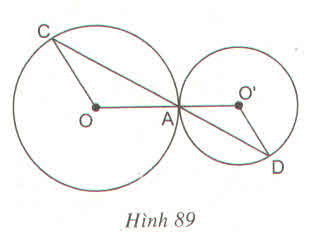
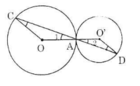
Ta có: OA = OC (bán kính) nên ΔOAC cân tại O.
![]()
Lại có O'A = O'D (bán kính) nên ΔO'AD cân tại O'

Vậy OC // O'D (có hai góc so le trong bằng nhau).

21 tháng 6 2017
a) ta có : VT = \(\left(\sqrt{3}-1\right)^2=3-2\sqrt{3}+1=4-2\sqrt{3}\) = VP
vậy \(\left(\sqrt{3}-1\right)^2=4-2\sqrt{3}\) (đpcm)
b) ta có : VT = \(\sqrt{4-2\sqrt{3}}-\sqrt{3}=\sqrt{\left(\sqrt{3}\right)^2-2.\sqrt{3}.1+1^2}-\sqrt{3}\)
= \(\sqrt{\left(\sqrt{3}-1\right)^2}-\sqrt{3}\) = \(\left|\sqrt{3}-1\right|-\sqrt{3}\) = \(\sqrt{3}-1-\sqrt{3}\) = 1 = VP
vậy \(\sqrt{4-2\sqrt{3}}-\sqrt{3}=-1\) (đpcm)
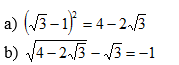
Ta có: OA = OC (bán kính) nên ΔOAC cân tại O.
suy ra C ^ = O A C ^ 1
Lại có O'A = O'D (bán kính) nên ΔO'AD cân tại O'
Vậy OC // O'D (có hai góc so le trong bằng nhau).