

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Ta có diện tích thiết diện là
S ( x ) = 1 2 πR 2 = 1 2 πx 2 4 - x = 1 2 π 4 x 2 - x 3
Thể tích của vật thể cần tìm là
V = ∫ 0 4 S ( x ) d x = 1 2 π ∫ 0 4 4 x 2 - x 3 dx = 1 2 π 4 3 x 3 - 1 4 x 4 | 0 4 = 32 π 3
Chọn đáp án D.

Đáp án C
V = ∫ 1 3 3 x 3 x 2 − 2 d x = 1 3 [ ( 3 x 2 − 2 ) 3 2 ] 3 1 = 124 3


Video không hỗ trỡ trên thiết bị của bạn!
Bài 2. Kỹ thuật tính Thể tích khối chóp - Phần 3 - Luyện thi THPTQG môn Toán - Thầy Nguyễn Quý Huy - MỤC TIÊU 8+
Video không hỗ trỡ trên thiết bị của bạn!
Bài 3. Rút gọn biểu thức - Luyện thi THPT QG môn Toán - Thầy Trần Xuân Trường - Mục tiêu 8+
Video không hỗ trỡ trên thiết bị của bạn!
Đề số 6: Bài tập Vận dụng - Phần 1 - Khóa LUYỆN ĐỀ môn TOÁN - Luyện thi THPT QG - Thầy Nguyễn Quý Huy
Video không hỗ trỡ trên thiết bị của bạn!
Bài 5. Bài tập Số phức - Phần 1.5 - Luyện thi THPTQG môn Toán - Thầy Nguyễn Quý Huy - MỤC TIÊU 8+
Video không hỗ trỡ trên thiết bị của bạn!
Bài 6. Kỹ thuật xử lý bài toán Tương giao đồ thị - Phần 2 - Luyện thi THPTQG môn Toán - Thầy Nguyễn Quý Huy - MỤC TIÊU 8+

Đáp án B.
Diện tích thiết diện là S x = x .2 9 − x 2 = 2 x 9 − x 2
Do đó thể tích của vật thể là V = ∫ 0 3 2 x 9 − x 2 d x
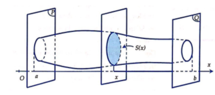

Đáp án C
Diện tích thiết diện là S = 2 x 2 x 2 − 1 .
Vậy thể tích V của vật là
V = 1 2 2 x 2 x 2 − 1 d x .
Đặt
u = 2 x 2 − 1 ⇒ d u = 2 x 2 x 2 − 1 d x ⇒ d x = u d u 2 x .
Vậy V = ∫ 1 7 u 2 d u = u 3 3 1 7 = 7 7 − 1 3 .

Đáp án D
Diện tích tam giác bằng 2 sin x 2 3 4 = 3 sin x .
Suy ra thể tích cần tích bằng V = ∫ 0 π 3 sin x d x = - 3 cos x 0 π = 2 3 .