K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
9 tháng 8 2016
a)\(\sqrt{x}>2\Leftrightarrow\sqrt{x^2}>2^2\Leftrightarrow x>4\)
\(\sqrt{x}< 1\Leftrightarrow\sqrt{x^2}< 1^2\Leftrightarrow x< 1\)
9 tháng 8 2016
a) \(\sqrt{x}>1\Leftrightarrow x>1\)
b) \(\sqrt{x}< 3\Leftrightarrow x< 9\)
Vì x không âm nên x={0;1;2;3;4;5;6;7;8}
9 tháng 8 2016
a)\(\sqrt{x}>1\Leftrightarrow\sqrt{x^2}>1^2\Leftrightarrow x>1\)
b)\(\sqrt{x}< 3\Leftrightarrow\sqrt{x^2}< 3^2\Leftrightarrow x< 9\)
BV
1
LH
19 tháng 6 2018
a) Bpt luôn đúng với mọi x không âm
b) đk: \(x\le2\)
Có: \(\sqrt{x}>\sqrt{2-x}\Leftrightarrow x>2-x\)
\(\Leftrightarrow2x>2\Leftrightarrow x>1\)
Kết hợp với đk, ta được: \(1< x\le2\)
5 tháng 8 2016
1. \(1=x^2+y^2\ge2xy\Rightarrow xy\le\frac{1}{2}\)
\(A=-2+\frac{2}{1+xy}\ge-2+\frac{2}{1+\frac{1}{2}}=-\frac{2}{3}\)
max A = -2/3 khi x=y=\(\frac{\sqrt{2}}{2}\)
5 tháng 8 2016
\(\frac{1}{xy}+\frac{1}{xz}=\frac{1}{x}\left(\frac{1}{y}+\frac{1}{z}\right)\ge\frac{1}{x}.\frac{4}{y+z}=\frac{4}{\left(4-t\right)t}=\frac{4}{4-\left(t-2\right)^2}\ge1\) với t = y+z => x =4 -t
5 tháng 6 2018
a/\(\sqrt{x}=7\)
\(\Leftrightarrow x=49\)
b/\(\Leftrightarrow x< 4\)(do x>0)
\(\Rightarrow x\varepsilon\left\{0;1;2;3\right\}\)
c/\(2x< 16\)
\(\Leftrightarrow x< 8\)
\(\Leftrightarrow x\varepsilon\left\{1;2;3;4;5;6;7\right\}\)
5 tháng 6 2018
a) \(2\sqrt{x}=14\Leftrightarrow\sqrt{x}=7\)
\(\Leftrightarrow x=7^2\Leftrightarrow x=49\)
b) \(\sqrt{x}< \sqrt{2}\Leftrightarrow x< 2\)
c) \(\sqrt{2x}< 4\)
Vì \(4=\sqrt{16}\text{ nên }\sqrt{2x}< 4\text{ có nghĩa là }\sqrt{2x}< 16\)
\(\Leftrightarrow2x< 16\)
\(\Leftrightarrow x< 8\left(x\ge0\right)\)
KN
2 tháng 11 2019
Ta có: \(\left(x-y\right)^2\ge0\)
\(\Leftrightarrow x^2-2xy+y^2\ge0\Rightarrow x^2+y^2\ge2xy\)
Tương tự: \(y^2+z^2\ge2yz\); \(x^2+z^2\ge2xz\)
Cộng từng vế của các BDDT trên:
\(2\left(xz+yz+xy\right)\le2\left(x^2+y^2+z^2\right)\)
\(\Leftrightarrow xy+yz+xz\le x^2+y^2+z^2\)
\(\Leftrightarrow3xy+3yz+3xz\le x^2+y^2+z^2+2xy+2yz+2xz\)
\(\Leftrightarrow3xy+3yz+3xz\le\left(x+y+z\right)^2\)
\(\Leftrightarrow3xy+3yz+3xz\le3^2=9\)
\(\Leftrightarrow xy+yz+xz\le3\)
Vậy \(D_{max}=3\Leftrightarrow x=y=z\)
KN
2 tháng 11 2019
Áp dụng BĐT Cauchy - Schwarz:
\(\left(x^2+y^2+z^2\right)\left(1+1+1\right)\)
\(=\left(x^2+y^2+z^2\right)\left(1^2+1^2+1^2\right)\ge\left(x+y+z\right)^2\)
\(\Rightarrow3\left(x^2+y^2+z^2\right)\ge3^2=9\)
\(\Rightarrow x^2+y^2+z^2\ge3\)
Vậy \(C_{min}=3\Leftrightarrow x=y=z=1\)
13 tháng 3 2019
a, Sửa đề \(x+y+z\le2+xy\)
Áp dụng bđt Cô-si có :
\(\left(x+y\right)+z\le\frac{\left(x+y\right)^2+1}{2}+\frac{z^2+1}{2}=\frac{x^2+2xy+y^2+1+z^2+1}{2}\)
\(=\frac{4+2xy}{2}\)
\(=2+xy\)
Dấu "=" khi x = 0 ; y = 1 ; z = 1
b,C/m tương tự câu a có \(x+y+z\le2+yz\)
\(x+y+z\le2zx\)
Ta có : \(P=\frac{x}{2+yz}+\frac{y}{2+zx}+\frac{z}{2+xy}\le\frac{x}{x+y+z}+\frac{y}{x+y+z}+\frac{z}{x+y+z}\)
\(=\frac{x+y+z}{x+y+z}=1\)
Dấu "=" khi x = 0 ; y = 1 ; z = 1
HT
Hoàng Thị Thu Huyền
Manager
3 tháng 4 2017
Với câu c, Thiên Anh nên thêm điều kiện để phần kết luận là: \(0\le x< 2.\)
WR
30 tháng 8 2017
\(\left(x+y+z\right)\left(\frac{1}{x}+\frac{1}{y}+\frac{1}{z}\right)\ge\frac{3\sqrt[3]{xyz}.3}{\sqrt[3]{xyz}}=9.\)
\(\Leftrightarrow\left(x+y+z\right)\left(\frac{xy+yz+xz}{xyz}\right)\ge9\Leftrightarrow xy+yz+xz\ge\frac{9xyz}{x+y+z}\)
lại có \(x+y+z=\sqrt{xyz}\Leftrightarrow\left(x+y+z\right)^2=xyz\)
=> đpcm
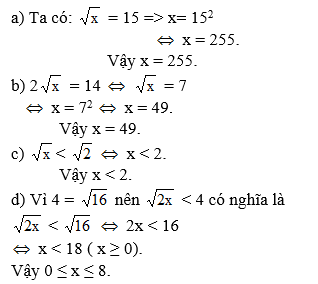
1 = √1, nên √x > 1 có nghĩa là √x > √1
Vì x ≥ 0 nên √x > √1 ⇔ x > 1. Vậy x > 1