Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a/ \(=lim\frac{1}{\sqrt{n+1}+\sqrt{n}}=\frac{1}{\infty}=0\)
b/ \(=lim\frac{6n+1}{\sqrt{n^2+5n+1}+\sqrt{n^2-n}}=\frac{6+\frac{1}{n}}{\sqrt{1+\frac{5}{n}+\frac{1}{n^2}}+\sqrt{1-\frac{1}{n}}}=\frac{6}{1+1}=3\)
c/ \(=lim\frac{6n-9}{\sqrt{3n^2+2n-1}+\sqrt{3n^2-4n+8}}=lim\frac{6-\frac{9}{n}}{\sqrt{3+\frac{2}{n}-\frac{1}{n^2}}+\sqrt{3-\frac{4}{n}+\frac{8}{n^2}}}=\frac{6}{\sqrt{3}+\sqrt{3}}=\sqrt{3}\)
d/ \(=lim\frac{\left(\frac{2}{6}\right)^n+1-4\left(\frac{4}{6}\right)^n}{\left(\frac{3}{6}\right)^n+6}=\frac{1}{6}\)
e/ \(=lim\frac{\left(\frac{3}{5}\right)^n-\left(\frac{4}{5}\right)^n+1}{\left(\frac{3}{5}\right)^n+\left(\frac{4}{5}\right)^n-1}=\frac{1}{-1}=-1\)
f/ Ta có công thức:
\(1+3+...+\left(2n+1\right)^2=\left(n+1\right)^2\)
\(\Rightarrow lim\frac{1+3+...+2n+1}{3n^2+4}=lim\frac{\left(n+1\right)^2}{3n^2+4}=lim\frac{\left(1+\frac{1}{n}\right)^2}{3+\frac{4}{n^2}}=\frac{1}{3}\)
g/ \(=lim\left(\frac{1}{1}-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+...+\frac{1}{n}-\frac{1}{n+1}\right)=lim\left(1-\frac{1}{n+1}\right)=1-0=1\)
h/ Ta có: \(1^2+2^2+...+n^2=\frac{n\left(n+1\right)\left(2n+1\right)}{6}\)
\(\Rightarrow lim\frac{n\left(n+1\right)\left(2n+1\right)}{6n\left(n+1\right)\left(n+2\right)}=lim\frac{2n+1}{6n+12}=lim\frac{2+\frac{1}{n}}{6+\frac{12}{n}}=\frac{2}{6}=\frac{1}{3}\)

Câu 4.
\(\lim \left( {{n^2}\sin \dfrac{{n\pi }}{5} - 2{n^3}} \right) = \lim {n^3}\left( {\dfrac{{\sin \dfrac{{n\pi }}{5}}}{n} - 2} \right) = - \infty \)
Vì \(\lim {n^3} = + \infty ;\lim \left( {\dfrac{{\sin \dfrac{{n\pi }}{5}}}{n} - 2} \right) = - 2 \)
\(\left| {\dfrac{{\sin \dfrac{{n\pi }}{5}}}{n}} \right| \le \dfrac{1}{n};\lim \dfrac{1}{n} = 0 \Rightarrow \lim \left( {\dfrac{{\sin \dfrac{{n\pi }}{5}}}{n} - 2} \right) = - 2\)
Câu 5.
Ta có: \(\left\{ \begin{array}{l} 0 \le \left| {{u_n}} \right| \le \dfrac{1}{{{n^2} + 1}} \le \dfrac{1}{n} \to 0\\ 0 \le \left| {{v_n}} \right| \le \dfrac{1}{{{n^2} + 2}} \le \dfrac{1}{n} \to 0 \end{array} \right. \to \lim {u_n} = \lim {v_n} = 0 \to \lim \left( {{u_n} + {v_n}} \right) = 0\)

a/ \(=lim\frac{3\left(\frac{2}{7}\right)^n-8}{4.\left(\frac{3}{7}\right)^n+5}=-\frac{8}{5}\)
b/ \(=lim\frac{6.4^n-\frac{2}{9}.6^n}{\frac{1}{2}.6^n+4.3^n}=lim\frac{6\left(\frac{4}{6}\right)^n-\frac{2}{9}}{\frac{1}{2}+4.\left(\frac{3}{6}\right)^n}=\frac{-\frac{2}{9}}{\frac{1}{2}}=-\frac{4}{9}\)
c/ \(=lim\frac{\left(-\frac{3}{5}\right)^n+2}{\left(\frac{1}{5}\right)^n-1}=\frac{2}{-1}=-2\)
d/ \(=lim\frac{n\left(n+1\right)}{2\left(n^2+n+1\right)}=lim\frac{1+\frac{1}{n}}{2+\frac{2}{n}+\frac{2}{n^2}}=\frac{1}{2}\)

Câu 2:
\(\frac{1}{1.2}+\frac{1}{2.3}+...+\frac{1}{n(n+1)}=\frac{2-1}{1.2}+\frac{3-2}{2.3}+...+\frac{(n+1)-n}{n(n+1)}\)
\(=1-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+...\frac{1}{n}-\frac{1}{n+1}\)
\(=1-\frac{1}{n+1}\)
\(\Rightarrow \lim_{n\to \infty}(\frac{1}{1.2}+\frac{1}{2.3}+...+\frac{1}{n(n+1)})=\lim_{n\to \infty}(1-\frac{1}{n+1})=1-\lim_{n\to \infty}\frac{1}{n+1}=1-0=1\)

a/
\(u_n=\dfrac{1}{\left(2-1\right)\left(2+1\right)}+\dfrac{1}{\left(3-1\right)\left(3+1\right)}+...+\dfrac{1}{\left(n-1\right)\left(n+1\right)}\)
\(u_n=\dfrac{1}{1.3}+\dfrac{1}{2.4}+\dfrac{1}{3.5}+\dfrac{1}{4.6}+...+\dfrac{1}{\left(n-2\right)n}+\dfrac{1}{\left(n-1\right)\left(n+1\right)}\)
\(u_n=\dfrac{1}{2}\left(1-\dfrac{1}{3}+\dfrac{1}{2}-\dfrac{1}{4}+\dfrac{1}{3}-\dfrac{1}{5}+...+\dfrac{1}{n-2}-\dfrac{1}{n}+\dfrac{1}{n-1}-\dfrac{1}{n+1}\right)\)
\(u_n=\dfrac{1}{2}\left(1+\dfrac{1}{2}-\dfrac{1}{n}-\dfrac{1}{n+1}\right)=\dfrac{1}{2}\left(\dfrac{3}{2}-\dfrac{1}{n}-\dfrac{1}{n+1}\right)\)
\(\Rightarrow lim\left(u_n\right)=lim\left(\dfrac{1}{2}\left(\dfrac{3}{2}-\dfrac{1}{n}-\dfrac{1}{n+1}\right)\right)=\dfrac{1}{2}.\dfrac{3}{2}=\dfrac{3}{4}\)
b/ \(u_n=\dfrac{1}{1^2+3}+\dfrac{1}{2^2+6}+...+\dfrac{1}{n^2+3n}=\dfrac{1}{1.4}+\dfrac{1}{2.5}+...+\dfrac{1}{n\left(n+3\right)}\)
\(u_n=\dfrac{1}{3}\left(1-\dfrac{1}{4}+\dfrac{1}{2}-\dfrac{1}{5}+\dfrac{1}{3}-\dfrac{1}{6}+\dfrac{1}{4}-\dfrac{1}{7}+...+\dfrac{1}{n}-\dfrac{1}{n+3}\right)\)
\(u_n=\dfrac{1}{3}\left(1+\dfrac{1}{2}+\dfrac{1}{3}-\dfrac{1}{n+1}-\dfrac{1}{n+2}-\dfrac{1}{n+3}\right)\)
\(\Rightarrow lim\left(u_n\right)=lim\left(\dfrac{1}{3}\left(1+\dfrac{1}{2}+\dfrac{1}{3}-\dfrac{1}{n+1}-\dfrac{1}{n+2}-\dfrac{1}{n+3}\right)\right)\)
\(\Rightarrow lim\left(u_n\right)=\dfrac{1}{3}\left(1+\dfrac{1}{2}+\dfrac{1}{3}\right)=\dfrac{11}{18}\)

Câu 1.
Vì \(\sqrt{2},\left(\sqrt{2}\right)^2,...,\left(\sqrt{2}\right)^n\) lập thành cấp số nhân có \(u_1=\sqrt{2}=q\) nên
\({u_n} = \sqrt 2 .\dfrac{{1 - {{\left( {\sqrt 2 } \right)}^n}}}{{1 - \sqrt 2 }} = \left( {2 - \sqrt 2 } \right)\left[ {{{\left( {\sqrt 2 } \right)}^n} - 1} \right] \to \lim {u_n} = + \infty \) vì \(\left\{{}\begin{matrix}a=2-\sqrt{2}>0\\q=\sqrt{2}>1\end{matrix}\right.\)
Câu 3.
Ta có biến đổi:
\(\lim \left( {\dfrac{{{n^2} - n}}{{1 - 2{n^2}}} + \dfrac{{2\sin {n^2}}}{{\sqrt n }}} \right) = \lim \dfrac{{{n^2} - n}}{{1 - 2{n^2}}} = \dfrac{1}{2}\)

\(=lim\frac{2.2^{5n}+3}{9.3^{5n}+1}=lim\frac{2.\left(\frac{2}{3}\right)^{5n}+3\left(\frac{1}{3}\right)^{5n}}{9+\left(\frac{1}{3}\right)^{5n}}=\frac{0}{9}=0\)
\(b=lim\frac{\left(-\frac{1}{3}\right)^n+4}{-1\left(-\frac{1}{3}\right)^n-2}=\frac{4}{-2}=-2\)
\(c=1+lim\frac{-n}{n^2+\sqrt{n^4+n}}=1+lim\frac{-\frac{1}{n}}{1+\sqrt{1+\frac{1}{n^3}}}=1+\frac{0}{2}=1\)
\(-2\le2cosn^2\le2\Rightarrow\frac{-2}{n^2+1}\le\frac{2cosn^2}{n^2+1}\le\frac{2}{n^2+1}\)
Mà \(lim\frac{-2}{n^2+1}=lim\frac{2}{n^2+1}=0\Rightarrow lim\frac{2cosn^2}{n^2+1}=0\)
\(d=lim\left[n\left(\sqrt{1-\frac{2}{n^2}}-1+1-\sqrt[3]{1+\frac{2}{n^2}}\right)\right]\)
\(=lim\left[n\left(\frac{-\frac{2}{n^2}}{\sqrt{1-\frac{2}{n^2}}+1}-\frac{\frac{2}{n^2}}{\sqrt[3]{\left(1+\frac{2}{n^2}\right)^2}+\sqrt[3]{1+\frac{2}{n^2}}+1}\right)\right]\)
\(=lim\left(\frac{-\frac{2}{n}}{\sqrt{1-\frac{2}{n^2}}+1}-\frac{\frac{2}{n}}{\sqrt[3]{\left(1+\frac{2}{n^2}\right)^2}+\sqrt[3]{1+\frac{2}{n^2}}+1}\right)=\frac{0}{2}-\frac{0}{1+1+1}=0\)

a) lim \(\frac{\left(2n+1\right)^2\left(n-1\right)}{\sqrt[3]{n^3+7n-2}}\)
= lim \(\left(2n+1\right)^2.\frac{\left(1-\frac{1}{n}\right)}{\sqrt[3]{1+\frac{7}{n^2}-\frac{2}{n^3}}}\)
\(=+\infty\)
b) lim \(\left(2n-1\right)\sqrt{\frac{2n^2+5}{n^4+n^2+2}}\)
= lim \(\left(2-\frac{1}{n}\right)\sqrt{\frac{2+\frac{5}{n^2}}{1+\frac{1}{n^2}+\frac{2}{n^4}}}\)
=2.2 = 4
c ) = lim \(n.\frac{n^2}{\sqrt[3]{\left(n^3+n^2\right)^2+n\sqrt[3]{n^3+n^2}+n^2}}\)
= lim \(n.\frac{1}{\sqrt[3]{\left(1+\frac{1}{n}\right)^2+\sqrt[3]{1+\frac{1}{n}}+1}}\)
\(=+\infty\)
Chọn D.
Với ∀x ∈ R ta có: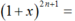
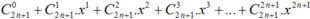
Lấy đạo hàm hai vế theo x ta được:
Thay x = -2 vào (1) ta được:
Từ yêu cầu bài toán ta có: 2n + 1 2017 ⇔ n = 2018.