
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

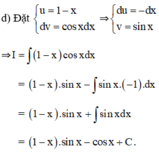

a) Áp dụng phương pháp tìm nguyên hàm từng phần:
Đặt u= ln(1+x)
dv= xdx
=> ,
Ta có: ∫xln(1+x)dx =
=
b) Cách 1: Tìm nguyên hàm từng phần hai lần:
Đặt u= (x2+2x -1) và dv=exdx
Suy ra du = (2x+2)dx, v = ex
. Khi đó:
∫(x2+2x - 1)exdx = (x2+2x - 1)exdx - ∫(2x+2)exdx
Đặt : u=2x+2; dv=exdx
=> du = 2dx ;v=ex
Khi đó:∫(2x+2)exdx = (2x+2)ex - 2∫exdx = ex(2x+2) – 2ex+C
Vậy
∫(x2+2x+1)exdx = ex(x2-1) + C
Cách 2: HD: Ta tìm ∫(x2-1)exdx. Đặt u = x2-1 và dv=exdx.
Đáp số : ex(x2-1) + C
c) Đáp số:
HD: Đặt u=x ; dv = sin(2x+1)dx
d) Đáp số : (1-x)sinx - cosx +C.
HD: Đặt u = 1 - x ;dv = cosxdx