Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

2, sin4x+cos5=0 <=> cos5x=cos\(\left(\frac{\pi}{2}+4x\right)\Leftrightarrow\orbr{\begin{cases}x=\frac{\pi}{2}+k2\pi\\x=-\frac{\pi}{18}+\frac{k2\pi}{9}\end{cases}\left(k\inℤ\right)}\)
ta có \(2\pi>0\Leftrightarrow k< >\frac{1}{4}\)do k nguyên nên nghiệm dương nhỏ nhất trong họ nghiệm \(\frac{\pi}{2}\)khi k=0
\(-\frac{\pi}{18}+\frac{k2\pi}{9}>0\Leftrightarrow k>\frac{1}{4}\)do k nguyên nên nghiệm dương nhỏ nhất trong họ nghiệm \(-\frac{\pi}{18}-\frac{k2\pi}{9}\)là \(\frac{\pi}{6}\)khi k=1
vậy nghiệm dương nhỏ nhất của phương trình là \(\frac{\pi}{6}\)
\(\frac{\pi}{2}+k2\pi< 0\Leftrightarrow k< -\frac{1}{4}\)do k nguyên nên nghiệm âm lớn nhất trong họ nghiệm \(\frac{\pi}{2}+k2\pi\)là \(-\frac{3\pi}{2}\)khi k=-1
\(-\frac{\pi}{18}+\frac{k2\pi}{9}< 0\Leftrightarrow k< \frac{1}{4}\)do k nguyên nên nghiệm âm lớn nhất trong họ nghiệm \(-\frac{\pi}{18}+\frac{k2\pi}{9}\)là \(-\frac{\pi}{18}\)khi k=0
vậy nghiệm âm lớn nhất của phương trình là \(-\frac{\pi}{18}\)

Câu 1:
Khong gian mẫu: \(C_{11}^3\)
Có 5 cặp bi cùng số, do đó có \(5\) cách chọn ra 1 cặp cùng số, viên còn lại có 9 cách chọn \(\Rightarrow\) có 45 cách chọn 3 viên có 2 viên cùng số (tất nhiên là ko thể 3 viên cùng số được)
Xác suất: \(P=\frac{C_{11}^3-45}{C_{11}^3}=\frac{8}{11}\)
Câu 2:
Không gian mẫu: \(9!\)
Xếp 4 bạn nam cạnh nhau và hoán vị, có \(4!\) cách
Coi 4 bạn nam này là 1 người, xếp hàng cùng 5 bạn nữ \(\Rightarrow\) có \(6!\) cách hoán vị
Vậy có \(4!.6!\) cách
Xác suất: \(P=\frac{4!.6!}{9!}=\frac{1}{21}\)

Trả lời :
Có 520 số chẵn gồm bốn chữ số đôi một khác nhau được lập từ các số 0,1,2,4,5,6,7.
# Hok tốt !

ĐK: \(x\ne\frac{k\pi}{2}\)
pt<=> \(8\sin x-\frac{4}{\sin x}=\frac{3}{\cos x}-\frac{3}{\sin x}\)
<=> \(4.\frac{2\sin^2x-1}{\sin x}=3.\frac{\sin x-\cos x}{\sin x.\cos x}\)
\(\Leftrightarrow4.\frac{\sin^2x-\cos^2x}{\sin x}=3.\frac{\sin x-\cos x}{\sin x.\cos x}\)
\(\Leftrightarrow4.\left(\sin x+\cos x\right)\left(\sin x-\cos x\right)=3\frac{\sin x-\cos x}{\cos x}\)
\(\Leftrightarrow\orbr{\begin{cases}\sin x-\cos x=0\left(1\right)\\4\left(\sin x+\cos x\right)=\frac{3}{\cos x}\left(2\right)\end{cases}}\)
(1) \(\Leftrightarrow\sqrt{2}\sin\left(x+\frac{\pi}{4}\right)=0\) ( tự giải nhé)
(2) \(\Leftrightarrow4\sin x.\cos x+4\cos x.\cos x=3\)
\(\Leftrightarrow2\sin2x+2\cos2x+2=3\)
\(\Leftrightarrow\sin2x+\cos2x=\frac{1}{2}\)
\(\Leftrightarrow\sqrt{2}\cos\left(2x+\frac{\pi}{4}\right)=\frac{1}{2}\)Tự giải nhé!

+ Số cách chọn 4 người bất kỳ từ nhóm người đó là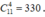
+ Số cách chọn 4 người từ nhóm đó mà không có nữ nào là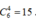
Vậy số cách chọn bốn người từ nhóm đó mà trong đó có ít nhất một nữ là: 330 – 15 = 315.
Chọn C.