Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ở trạng thái kích thích thứ nhất: n = 2
Trạng thái kích thích thứ ba: n = 4
Ta có:
\(r_n=r_0.n^2\)
\(\Rightarrow r_2=r_0.4\)
\(r_4=r_0.16\)
\(\Rightarrow \dfrac{r_4}{r_2}=4\Rightarrow r_4=r_2.4=8,48.10^{-10}(m)\)
Chọn A.

\(\frac{r}{r_0}=\frac{2,2.10^{-10}}{5,3.10^{-11}} \approx 4.\)
=> \(r = 4r_0 = 2^2 r_0.\) Tức là electron nhảy lên trạng thái dừng L (n = 2).

Đáp án A
Áp dụng công thức tính bán kính quỹ đạo dừng trong mẫu nguyên tử Bo ![]()

Bán kính nguyên tử hiđrô: \(r_n=n^2r_0.\)
Bán kính quỹ đạo dừng N ứng với n = 4
=> \(r_N=r_4= 4^2.5,3.10^{-11}= 84,8.10^{-11}m.\)

Bán kính quỹ đạo dừng của hiđrô: \(r_n=n^2r_0.\)
Bán kính quỹ đạo dừng M ứng với n = 3
=> \(r_M=r_3= 3^2.5,3.10^{-11}=47,7.10^{-11}m.\)
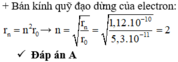
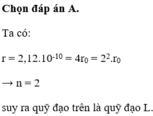
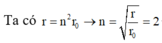
- Trạng thái kích thích thứ 3 ứng với quỹ đạo dừng N (K,L,M,N).
- Tức là n = 4. Vậy bán kính là :