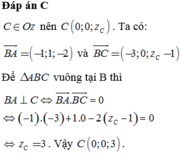Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

19.
Phương trình mặt phẳng theo đoạn chắn:
\(\frac{x}{3}+\frac{y}{-4}+\frac{z}{-2}=1\)
\(\Leftrightarrow4x-3y-6z-12=0\)
20.
Phương trình mặt phẳng (ABC) theo đoạn chắn:
\(\frac{x}{1}+\frac{y}{2}+\frac{z}{3}=1\)
\(\Leftrightarrow6x+3y+2z-6=0\)
Chẳng đáp án nào đúng cả, chắc bạn ghi nhầm đáp án C số 1 thành số 0 :)
15.
\(2\left(x-2\right)-5\left(y+3\right)+1\left(z+2\right)=0\)
16.
\(\overrightarrow{n_1}=\left(1;1;-1\right)\) ; \(\overrightarrow{n_2}=\left(1;-1;1\right)\)
\(\left[\overrightarrow{n_1};\overrightarrow{n_2}\right]=\left(0;-2;-2\right)=-2\left(0;1;1\right)\)
Phương trình (P):
\(1\left(y-1\right)+1\left(z-1\right)=0\Leftrightarrow y+z-2=0\)
17.
\(\overrightarrow{n_P}=\left(1;-1;1\right)\) ; \(\overrightarrow{n_Q}=\left(3;2;-12\right)\)
\(\left[\overrightarrow{n_P};\overrightarrow{n_Q}\right]=\left(10;15;5\right)=5\left(2;3;1\right)\)
Phương trình mặt phẳng (R):
\(2x+3y+z=0\)
18.
\(\overrightarrow{MN}=\left(0;-2;3\right);\overrightarrow{MP}=\left(-2;1;3\right)\)
\(\left[\overrightarrow{MN};\overrightarrow{MP}\right]=\left(-9;-6;-4\right)=-1\left(9;6;4\right)\)
Phương trình:
\(9\left(x-2\right)+6\left(y-2\right)+4z=0\)
\(\Leftrightarrow9x+6y+4z-30=0\)

4.
(P) nhận \(\left(2;-1;-1\right)\) là 1 vtpt
Phương trình (d) qua A và vuông góc (P): \(\left\{{}\begin{matrix}x=2+2t\\y=1-t\\z=4-t\end{matrix}\right.\)
Hình chiếu A' của A lên (P) là giao điểm d và (P) nên tọa độ thỏa mãn:
\(2\left(2+2t\right)-\left(1-t\right)-\left(4-t\right)+7=0\Rightarrow t=-1\)
\(\Rightarrow A'\left(0;2;5\right)\)
5.
Pt hoành độ giao điểm: \(lnx=0\Rightarrow x=1\)
Diện tích: \(S=\int\limits^e_1lnxdx-\int\limits^1_{\frac{1}{e}}lnxdx\)
Xét \(I=\int lnxdx\Rightarrow\left\{{}\begin{matrix}u=lnx\\dv=dx\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}du=\frac{dx}{x}\\v=x\end{matrix}\right.\)
\(\Rightarrow I=x.lnx-\int dx=xlnx-x\)
\(\Rightarrow S=\left(xlnx-x\right)|^e_1-\left(xlnx-x\right)|^1_{\frac{1}{e}}=1-\left(-1+\frac{2}{e}\right)=2-\frac{2}{e}\)
6.
Pt đường thẳng bị thiếu mẫu số đầu tiên
7.
Đề bài thiếu
1.
\(\left\{{}\begin{matrix}z_1+z_2=6\\z_1z_2=\left(3+2i\right)\left(3-2i\right)=13\end{matrix}\right.\)
\(\Rightarrow z_1;z_2\) là nghiệm của pt: \(z^2-6z+13=0\)
2.
\(\overrightarrow{BC}=\left(1;-2;-5\right)\)
Phương trình (P):
\(1\left(x-2\right)-2\left(y-1\right)-5\left(z+1\right)=0\)
\(\Leftrightarrow x-2y-5z-5=0\)
3.
\(I=\int\limits^0_{-1}x^2\left(x^2+2x+1\right)dx=\int\limits^0_{-1}\left(x^4+2x^3+x^2\right)dx=\left(\frac{1}{5}x^5+\frac{1}{2}x^4+\frac{1}{3}x^2\right)|^0_{-1}=\frac{1}{30}\)

6.
Mặt phẳng Oxz có pt: \(y=0\)
Khoảng cách từ I đến Oxz: \(d\left(I;Oxz\right)=\left|y_I\right|=2\)
\(\Rightarrow R=2\)
Phương trình mặt cầu:
\(\left(x-1\right)^2+\left(y-2\right)^2+\left(z-3\right)^2=4\)
7.
Mặt phẳng (Q) nhận \(\left(1;-2;3\right)\) là 1 vtpt nên cũng nhận các vecto có dạng \(\left(k;-2k;3k\right)\) là vtpt
Bạn có ghi nhầm đề bài ko nhỉ? Thế này thì cả C và D đều ko phải vecto pháp tuyến của (Q)
4.
Đường thẳng d nhận \(\left(1;-2;2\right)\) là 1 vtcp
Gọi (P) là mặt phẳng qua M và vuông góc d \(\Rightarrow\) (P) nhận \(\left(1;-2;2\right)\) là 1 vtpt
Phương trình (P): \(1\left(x-2\right)-2\left(y-3\right)+2\left(z+1\right)=0\)
\(\Leftrightarrow x-2y+2z+6=0\)
Pt d dạng tham số: \(\left\{{}\begin{matrix}x=4+t\\y=1-2t\\z=5+2t\end{matrix}\right.\)
Tọa độ hình chiếu M' của M lên d là giao của d và (P) nên thỏa mãn:
\(4+t-2\left(1-2t\right)+2\left(5+2t\right)+6=0\) \(\Rightarrow t=-2\)
\(\Rightarrow M'\left(2;5;1\right)\)
5.
(P) nhận \(\left(2;3;1\right)\) là 1 vtpt
Gọi d là đường thẳng qua I và vuông góc (P)
\(\Rightarrow\) d nhận \(\left(2;3;1\right)\) là 1 vtcp
Phương trình tham số d: \(\left\{{}\begin{matrix}x=1+2t\\y=-2+3t\\z=1+t\end{matrix}\right.\)
H là giao điểm của d và (P) nên tọa độ thỏa mãn:
\(2\left(1+2t\right)+3\left(-2+3t\right)+1+t-11=0\) \(\Rightarrow t=1\)
\(\Rightarrow H\left(3;1;2\right)\)

\(\overrightarrow{PQ}=\left(-1;-1;4\right)\)
\(\overrightarrow{n_{\left(P\right)}}=\left(3;2;-1\right)\)
\(\Rightarrow\left[\overrightarrow{PQ};\overrightarrow{n_{\left(P\right)}}\right]=\left(-7;11;1\right)\)
\(\Rightarrow\) Mặt phẳng \(\left(\Delta\right)\) nhận \(\left(-7;11;1\right)\) là 1 vtpt
Phương trình:
\(-7\left(x-2\right)+11\left(y-0\right)+1\left(z+1\right)=0\)
\(\Leftrightarrow-7x+11y+z+15=0\)

Ta có : \(\overrightarrow{AB}=\left(-a;b;0\right)\)
và \(\overrightarrow{AC}=\left(-a;0;c\right)\)
Vì \(\overrightarrow{AB}.\overrightarrow{AC}=a^2>0\) nên góc \(\widehat{BAC}\) là góc nhọn
Lập luận tương tự chứng minh được các góc \(\widehat{B}\) và \(\widehat{C}\) cũng là góc nhọn

1/ \(\overrightarrow{AI}=\left(1;1;-3\right)\)
Do (P) tiếp xúc với (S) tại A \(\Rightarrow AI\perp\left(P\right)\Rightarrow\left(P\right)\) nhận \(\overrightarrow{AI}\) là một vtpt
\(\Rightarrow\) phương trình (P):
\(1\left(x-2\right)+1\left(y-1\right)-3\left(z-2\right)=0\Leftrightarrow x+y-3z+3=0\)
2/ \(\overrightarrow{u_d}=\left(2;-1;4\right)\) ; \(\overrightarrow{n_{\left(P\right)}}=\left(1;0;0\right)\)
Gọi A là giao điểm của d và (P) có pt \(x+3=0\)
\(\Rightarrow x_A=-3\) (suy từ pt (P)); \(y_A=-3;z_A=-5\) (thay \(x_A\) vào pt d) \(\Rightarrow A\left(-3;-3;-5\right)\)
Gọi (Q) là mặt phẳng qua d và vuông góc (P) \(\Rightarrow\left(Q\right)\) chứa A và (Q) có 1 vtpt là \(\overrightarrow{n_{\left(Q\right)}}=\left[\overrightarrow{u_d};\overrightarrow{n_{\left(P\right)}}\right]=\left(0;4;1\right)\)
\(\Rightarrow\) pt (Q): \(0\left(x+3\right)+4\left(y+3\right)+1\left(z+5\right)=0\Leftrightarrow4y+z+17=0\)
Gọi \(d'\) là hình chiếu của d lên (P) \(\Rightarrow\) \(d'\)có một vecto chỉ phương là \(\overrightarrow{u_{d'}}=\left[\overrightarrow{n_{\left(P\right)}};\overrightarrow{n_{\left(Q\right)}}\right]=\left(0;-1;4\right)\) và \(d'\) qua A
\(\Rightarrow\) pt đường thẳng \(d':\) \(\left\{{}\begin{matrix}x=-3+0.t\\y=-3+\left(-1\right).t\\z=-5+4.t\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x=-3\\y=-3-t\\z=-5+4t\end{matrix}\right.\) (1)
Đến đây thì đừng bối rối vì không thấy đáp án, vì việc viết pt tham số của đường thẳng sẽ ra các kết quả khác nhau khi ta chọn điểm khác nhau (một đường thẳng chứa vô số điểm vì thế cũng có vô số cách viết 1 pt tham số của đường thẳng)
Kiểm tra đáp án chính xác bằng cách loại trừ, đầu tiên nhìn vào vecto chỉ phương \(\left(0;-1;4\right)\) \(\Rightarrow\) loại đáp án B và C
Đáp án A họ sử dụng điểm có tọa độ \(\left(-3;-5;-3\right)\) để viết, thay thử 3 tọa độ này vào hệ (1), dòng 2 cho \(-5=-3-t\Rightarrow t=2\) ; dòng 3 cho \(-3=-5+4t\Rightarrow t=\dfrac{1}{2}\ne2\). Vậy A sai nốt, D là đáp án đúng (bạn có thể thay tạo độ \(\left(-3;-6;7\right)\) vào (1) sẽ thấy đúng)
3/ Gọi \(d\) đi qua A vuông góc \(\left(P\right)\)
Ta có \(\overrightarrow{n_{\left(P\right)}}=\left(1;3;-1\right)\Rightarrow\) chọn \(\overrightarrow{u_d}=\overrightarrow{n_{\left(P\right)}}=\left(1;3;-1\right)\) là 1vecto chỉ phương của d
\(\Rightarrow\) pt tham số d có dạng: \(\left\{{}\begin{matrix}x=2+t\\y=3+3t\\z=-t\end{matrix}\right.\) (2)
Lại giống câu trên, họ chọn 1 điểm khác để viết, nhưng câu này thì loại trừ đơn giản hơn vì chi có đáp án B là đúng vecto chỉ phương, chọn luôn ko cần suy nghĩ
Nếu ko tin, thay thử điểm \(\left(1;0;1\right)\) trong câu B vào (2)
Dòng 1 cho \(1=2+t\Rightarrow t=-1\)
Dòng 2 cho \(0=3+3t\Rightarrow t=-1\)
Dòng 3 cho \(1=-t\Rightarrow t=-1\)
3 dòng cho 3 giá trị t giống nhau, vậy điểm đó thuộc d \(\Rightarrow\) đáp án đúng

3.
\(d\left(I;\left(P\right)\right)=\frac{\left|-1-4-2-2\right|}{\sqrt{1^2+2^2+2^2}}=3\)
Áp dụng định lý Pitago:
\(R=\sqrt{5^2+3^2}=\sqrt{34}\)
Pt mặt cầu:
\(\left(x+1\right)^2+\left(y-2\right)^2+\left(z+1\right)^2=34\)
\(\Leftrightarrow x^2+y^2+z^2+2x-4y+2z-28=0\)
4.
\(\left(\alpha\right)\) nhận \(\left(2;-3;-4\right)\) là 1 vtpt và tất cả các vecto có dạng \(\left(2k;-3k;-4k\right)\) cũng là các vecto pháp tuyến với \(k\ne0\) (bạn tự tìm đáp án phù hợp)
5.
\(\overrightarrow{AB}=\left(3;-6;0\right)\) ; \(\overrightarrow{AC}=\left(5;3;3\right)\)
\(\Rightarrow\left[\overrightarrow{AB};\overrightarrow{AC}\right]=\left(-18;-9;39\right)=-3\left(6;3;-13\right)\)
Mặt phẳng (ABC) nhận \(\left(6;3;-13\right)\) là 1 vtpt
Phương trình:
\(6\left(x+1\right)+3\left(y-2\right)-13\left(z-3\right)=0\)
\(\Leftrightarrow6x+3y-13z+39=0\)
1.
\(\overrightarrow{IA}=\left(4;2;6\right)\Rightarrow R^2=IA^2=4^2+2^2+6^2=56\)
Pt mặt cầu:
\(\left(x-1\right)^2+\left(y+3\right)^2+\left(z+2\right)^2=56\)
Dạng khai triển:
\(x^2+y^2+z^2-2x+6y+4z-42=0\)
2.
\(\overrightarrow{BA}=\left(10;2;-12\right)\Rightarrow R=\frac{AB}{2}=\frac{1}{2}\sqrt{10^2+2^2+12^2}=\sqrt{62}\)
Gọi I là trung điểm AB \(\Rightarrow I\left(1;1;1\right)\)
Pt mặt cầu:
\(\left(x-1\right)^2+\left(y-1\right)^2+\left(z-1\right)^2=62\)
\(\Leftrightarrow x^2+y^2+z^2-2x-2y-2z-59=0\)

8.
\(a^2+9b^2=10ab\Leftrightarrow a^2+6ab+9b^2=16ab\)
\(\Leftrightarrow\left(a+3b\right)^2=16ab\)
\(\Rightarrow log\left(a+3b\right)^2=log\left(16ab\right)\)
\(\Rightarrow2log\left(a+3b\right)=log16+loga+logb\)
\(\Leftrightarrow log\left(a+3b\right)-\frac{log4^2}{2}=\frac{loga+logb}{2}\)
\(\Leftrightarrow log\left(a+3b\right)-log4=\frac{loga+logb}{2}\)
\(\Leftrightarrow log\frac{a+3b}{4}=\frac{loga+logb}{2}\)
9.
Tung độ của điểm M bằng 0 nên nó nằm trên mặt phẳng Oxz
5.
\(z^2+4z+5=0\Leftrightarrow\left(z+2\right)^2=-1=i^2\)
\(\Rightarrow\left[{}\begin{matrix}z+2=i\\z+2=-1\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}z_2=-2+i\\z_1=-2-i\end{matrix}\right.\)
\(\Rightarrow w=z_1-2z_2=2-3i\)
\(\Rightarrow\left|w\right|=\sqrt{2^2+\left(-3\right)^2}=\sqrt{13}\)
6.
\(\overrightarrow{AB}=\left(1;2;1\right)\Rightarrow\) mặt phẳng (P) nhận (1;2;1) là 1 vtpt
Pt (P): \(1\left(x-0\right)+2\left(y-1\right)+1\left(z-1\right)=0\)
\(\Leftrightarrow x+2y+z-3=0\)
7.
Đề chắc ghi sai, có phải đề đúng là xác suất để ko có học sinh nam nào ngồi cạnh nhau?
Xếp bất kì: có \(9!\) cách
Xếp 6 bạn nữ có \(6!\) cách, 6 bạn nữ này tạo ra 7 vị trí trống, xếp 3 bạn nam vào các vị trí trống đó có \(A_7^3\) cách
Xác suất: \(P=\frac{6!.A_7^3}{9!}=\frac{5}{12}\)