Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

S A B M N C
Dùng định lý hàm số Cosin tính được \(MN=2a\sqrt{3}\)
\(AM=2a\sqrt{2},AN=2a\). Tam giác vuông SAC có SC=2SA nên góc ASC =60 độ suy ra tam giác AMN vuông tại A.
Gọi H là trung điểm của MN, vì SA=SM=SN và tam giác AMN vuông tại A \(\Rightarrow SH\perp\left(AMN\right)\), tính được SH=a
Tính được \(V_{S.AMN}=\frac{2\sqrt{2}a^3}{3}\)
\(\frac{V_{S.AMN}}{V_{S.ABC}}=\frac{SM.SN}{SB.SC}=\frac{1}{3}\) \(\Rightarrow V_{S.ABC}=2\sqrt{2}a^3\)
Vậy d(C;(SAB)) =\(\frac{3V_{S.ABC}}{S_{\Delta SAB}}=\frac{6a^3\sqrt{2}}{3a^2}=2a\sqrt{2}\)

Khoảng cách từ A đến mặt phẳng (P) là :
\(h=d_{\left(A,\left(P\right)\right)}=\frac{\left|1.2+\left(-2\right).\left(-2\right)+2.1+5\right|}{\sqrt{1^2+\left(-2\right)^2+2^2}}=4\)
Gọi r là bán kính của đường tròn thiết diện thì ta có \(2\pi r=6\pi\Rightarrow r=3\)
Gọi R là bán kính mặt cầu cần tìm, ta có : \(R^2=h^2+r^2=4^2+3^2=25\)
Vậy phương trình mặt cầu cần tìm là : \(\left(x-1\right)^2+\left(y+2\right)^2+\left(z-1\right)^2=25\)








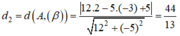
d(M,( β )) = 28/5