Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1) Ta có : \(\frac{2016a+b+c+d}{a}=\frac{a+2016b+c+d}{b}=\frac{a+b+2016c+d}{c}=\frac{a+b+c+2016d}{d}\)
Trừ 4 vế với 2015 ta được : \(\frac{a+b+c+d}{a}=\frac{a+b+c+d}{b}=\frac{a+b+c+d}{c}=\frac{a+b+c+d}{d}\)
Nếu a + b + c + d = 0
=> a + b = -(c + d)
=> b + c = (-a + d)
=> c + d = -(a + b)
=> d + a = (-b + c)
Khi đó M = (-1) + (-1) + (-1) + (-1) = - 4
Nếu a + b + c + d\(\ne0\Rightarrow\frac{1}{a}=\frac{1}{b}=\frac{1}{c}=\frac{1}{d}\Rightarrow a=b=c=d\)
Khi đó M = 1 + 1 + 1 + 1 = 4
2) a) Ta có : \(\hept{\begin{cases}\left|x+2013\right|\ge0\forall x\\\left(3x-7\right)^{2004}\ge0\forall y\end{cases}\Rightarrow\left|x+2013\right|+\left(3x-7\right)^{2014}\ge0}\)
Dấu "=" xảy ra \(\hept{\begin{cases}x+2013=0\\3y-7=0\end{cases}\Rightarrow\hept{\begin{cases}x=-2013\\y=\frac{7}{3}\end{cases}}}\)
b) 72x + 72x + 3 = 344
=> 72x + 72x.73 = 344
=> 72x.(1 + 73) = 344
=> 72x = 1
=> 72x = 70
=> 2x = 0 => x = 0
c) Ta có :
\(\frac{7}{2x+2}=\frac{3}{2y-4}=\frac{5}{x+4}\Leftrightarrow\frac{7}{2x+2}=\frac{3}{2y-4}=\frac{10}{2x+8}=\frac{7-10}{2x+2-2x-8}=\frac{1}{2}\)(dãy tỉ số bằng nhau)
=> 2x + 2 = 14 => x = 6 ;
2y - 4 = 6 => y = 5 ;
6 + 5 + z = 17 => z = 6
Vậy x = 6 ; y = 5 ; z = 6
3) a) Ta có : \(\frac{a+b+c}{a+b-c}=\frac{a-b+c}{a-b-c}=\frac{a+b+c-a+b-c}{a+b-c-a+b+c}=\frac{2b}{2b}=1\)(dãy ti số bằng nhau)
=> a + b + c = a + b - c => a + b + c - a - b + c = 0 => 2c = 0 => c = 0;
Lại có : \(\frac{a+b+c}{a+b-c}-1=\frac{a-b+c}{a-b-c}-1\Leftrightarrow\frac{2c}{a+b-c}=\frac{2c}{a-b-c}\Rightarrow a+b-c=a-b-c\) => b = 0
Vậy c = 0 hoặc b = 0
c) Ta có : \(\frac{a+b}{c}=\frac{b+c}{a}=\frac{a+c}{b}=\frac{a+b+b+c+a+c}{c+a+b}=2\)(dãy tỉ số bằng nhau)
=> \(\hept{\begin{cases}a+b=2c\\b+c=2a\\a+c=2b\end{cases}}\)
Khi đó P = \(\left(1+\frac{c}{b}\right)\left(1+\frac{a}{c}\right)\left(1+\frac{b}{a}\right)=\frac{b+c}{b}.\frac{c+a}{c}=\frac{a+b}{a}=\frac{2a.2b.2c}{abc}=8\)
Vậy P = 8
2. b) \(7^{2x}+7^{2x+3}=344\)
\(7^{2x}\cdot\left(1+7^3\right)=344\)
\(7^{2x}\cdot\left(1+343\right)=344\)
\(7^{2x}\cdot344=344\)
\(7^{2x}=1\)
\(7^{2x}=7^0\)
\(2x=0\)
\(x=0\)

a) \(\frac{x}{2}=\frac{y}{5}=\frac{x+y}{2+5}=\frac{70}{7}=10\)\(\Rightarrow x=20;y=50\)
b)\(2x=3y\Rightarrow\frac{x}{3}=\frac{y}{2}\)
\(\Rightarrow\frac{2x}{6}=\frac{y}{2}=\frac{2x+y}{6+2}=\frac{64}{8}=8\)\(\Rightarrow x=24;y=16\)
c) \(\frac{x}{2}=\frac{y}{3}=k\Rightarrow x=2k;y=3k\)
xy = 6k2 = 54 \(\Rightarrow\)k2 = 9 \(\Rightarrow\) k = 3 hoặc k = -3
Khi đó : x = 6 ; y = 9 hoặc x = -6 ; y = -9

\(A=\left|x+\frac{1}{2}\right|-1\)
ta có \(\left|x+\frac{1}{2}\right|\ge0\forall x\in R\)
\(\Rightarrow\left|x+\frac{1}{2}\right|-1\ge-1\forall x\in R\)
\(\Rightarrow A\ge-1\)
\(A=-1\Leftrightarrow x+\frac{1}{2}=0\Leftrightarrow x=-\frac{1}{2}\)
Vậy GTNN của A=-1 tại x=-1/2

1. a, \(2^{x+2}.3^{x+1}.5^x=10800\)
\(2^x.2^2.3^x.3.5^x=10800\)
\(\Rightarrow\left(2.3.5\right)^x.12=10800\)
\(\Rightarrow30^x=\frac{10800}{12}=900\)
\(\Rightarrow30^x=30^2\)
\(\Rightarrow x=2\)
b,\(3^{x+2}-3^x=24\)
\(\Rightarrow3^x\left(3^2-1\right)=24\)
\(\Rightarrow3^x.8=24\)\(\Rightarrow3^x=3^1\Rightarrow x=1\)
2, c, Áp dụng BĐT \(\left|a\right|+\left|b\right|\ge\left|a+b\right|\)
Dấu bằng xảy ra khi \(ab\ge0\)
Ta có: \(\left|x-2017\right|=\left|2017-x\right|\)
\(\Rightarrow\left|x-1\right|+\left|2017-x\right|\ge\left|x-1+2017-x\right|\)\(=\left|2016\right|=2016\)
Dấu bằng xảy ra khi \(\left(x-1\right)\left(2017-x\right)\ge0\)\(\Rightarrow2017\ge x\ge1\)
Vậy \(Min_{BT}=2016\)khi \(2017\ge x\ge1\)
d, Áp dụng BĐT \(\left|a\right|-\left|b\right|\le\left|a-b\right|\forall a,b\inℝ\)
Dấu bằng xảy ra khi \(b\left(a-b\right)\ge0\)
Ta có \(B=\left|x-2018\right|-\left|x-2017\right|\le\left|x-2018-x+2017\right|\)
\(\Rightarrow B\le1\)
Dấu bằng xảy ra khi \(\left(x-2017\right)\left[\left(x-2018\right)-\left(x-2017\right)\right]\ge0\)
\(\Rightarrow x\le2017\)
Vậy \(Max_B=1\) khi \(x\le2017\)
để BT \(\frac{5}{\sqrt{2x+1}+2}\) nguyên thì \(\sqrt{2x+1}+2\inƯ\left(5\right)\)
suy ra \(\sqrt{2x+1}+2\in\left\{-5;-1;1;5\right\}\)
\(\Rightarrow\sqrt{2x+1}\in\left\{-7;-3;-1;3\right\}\)
Mà \(\sqrt{2x+1}\ge0\) nên \(\sqrt{2x+1}\)chỉ có thể bằng 3
\(\Rightarrow2x+1=9\Rightarrow x=4\)( thỏa mãn điều kiện \(x\ge-\frac{1}{2}\))
Đây là cách lớp 9. Mk đang phân vân ko biết giải theo cách lớp 7 thế nào!!!!

+) \(\left|x-\frac{4}{7}\right|\ge0\)
\(A=\left|x-\frac{4}{7}\right|-\frac{1}{2}\ge\frac{-1}{2}\)
min A=-1/2 tại x=4/7
+) \(\left|x+\frac{5}{3}\right|\ge0\)
\(B=-\left|x+\frac{5}{3}\right|\le0\)
max B=0 khi x=-5/3

a) A = 3 * /1-2x/-5
Ta có:
3|1-2x| >/ 0
=> 3|1-2x| -5 >/ -5
=> GTNN của A là -5
b)-B=3/4-_ /2_3x/
Chả hiểu
c)C=(2x^2+1)^4-3
Ta có: 2x^2 >/ 0
2x^2 +1 >/ 1
(2x^2 +1)^4 >/ 1^4
(2x^2 +1)^4 -3 >/ 1 -3
(2x^2 +1)^4 >/ -2
Vậy GTNN của C là -2
d) D=/x-1/2/ + (y+7)^2+11
Ta có:
|x-1/2| >/ 0 (1)
và (y+7)^2 >/ 0
=> (y+7)^2 +11 >/ 11 (2)
Cộng vế với vế (1) và (2) ta được:
|x-1/2| + (y+7)^2 +11 >/ 11
Vậy GTNN của D là 11

a)\(x=\dfrac{-14\cdot52}{72}\\ x=\dfrac{-91}{9}\)
b)\(x=\dfrac{120\cdot7.2}{70}\\ x=\dfrac{432}{35}\)
c)\(x=\dfrac{2\dfrac{2}{3}\cdot8.5}{5}\\ x=\dfrac{68}{15}\)
d)\(x=\dfrac{4\dfrac{2}{5}\cdot9.5}{8}\\ x=\dfrac{209}{40}\)

Câu 1:
C.14
Câu 2:
B.\(\dfrac{-2}{3}\)\(x^4\)\(y^4\)
Câu 3:
C.\(72^0\)
Câu 4: Không có hình nên mình tạm thời không làm nha
Câu 1: Thay \(x=-1;y=2\) vào bt ta có:
\(5.\left(-1\right)^2+6.2-3=5.1+12-3=14\)
Vậy chọn ý C
Câu 2: Tính:
\(-\dfrac{1}{3}x^2y.2x^2y^3=\left(-\dfrac{1}{3}.2\right)\left(x^2.x^2\right)\left(y.y^3\right)\)
\(=-\dfrac{2}{3}x^4y^4\)
Vậy chịn ý B
Câu 3: gọi tam giác đó là: \(\Delta ABC\) cân tại A, có: \(\widehat{A}=36^o\)
Ta có: \(\widehat{A}+\widehat{B}+\widehat{C}=180^o\) (tổng 3 góc troq 1 tam giác)
hay \(36^o+\widehat{B}+\widehat{C}=180^o\)
\(\Rightarrow\widehat{B}+\widehat{C}=180^o-36^o=144^o\)
mà \(\widehat{B}=\widehat{C}\) (\(\Delta ABC\) cân tại A)
\(\Rightarrow\widehat{B}=\widehat{C}=\dfrac{144^o}{2}=72^o\)
Vậy chọn ý C
Câu 4: k có hình!
Ta có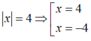
+ Trường hợp 1: x = 4 : Thay x = 4 vào biểu thức ta có:
5 . 4 2 - 2 . 4 - 18 = 5 . 16 - 8 - 18 = 80 - 8 - 18 = 54
Vậy B = 54 tại x = 4
+ Trường hợp 2: x = -4 : Thay x = -4 vào biểu thức ta có:
5 . - 4 2 - 2 . ( - 4 ) - 18 = 5 . 16 + 8 - 18 = 80 + 8 - 18 = 70
Vậy B = 70 tại x = -4
Với |x| = 4 thì B = 54 hoặc B = 70
Chọn đáp án C