Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

+ Ta có T = 2 π l g → g ¯ = 2 π 2 l ¯ T 2 ¯ = 9 , 64833 m / s 2
→ Sai số tuyệt đối của phép đo: Δ g = g ¯ Δ l l ¯ + 2 Δ T T ¯ = 0 , 0314 m / s 2
Ghi kết quả: T = 9 , 648 ± 0 , 031 m / s 2
Đáp án B

Phương pháp: Sử dụng công thức tính chu kì dao động của con lắc đơn và công thức tính sai số trong thực hành thí nghiệm
Cách giải:
Công thức xác định độ lớn gia tốc trọng trường:
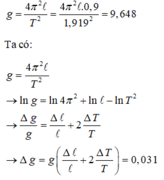
Đáp án A

Đáp án A
Phương pháp: Sử dụng công thức tính chu kì dao động của con lắc đơn và công thức tính sai số trong thực hành thí nghiệm
Cách giải :
Công thức xác định độ lớn gia tốc trọng trường:
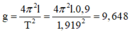
Ta có:
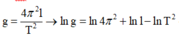
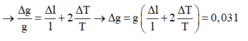

Ta có:
Con lắc thực hiện 100 dao động hết 31,4 (s)
Lại có gốc thời gian là lúc quả cầu có li độ 2cm và đang chuyển động theo chiều dương của trục tọa độ với vận tốc có độ lớn
và

Đáp án A
Phương pháp: Sử dụng công thức tính chu kì con lắc đơn T= 2 π l g kết hợp với lí thuyết sai số trong thí nghiệm thực hành
Cách giải:
Chu kì của con lắc đơn: T= 2 π l g
Gia tốc rơi tự do được xác định theo công thức:
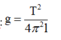
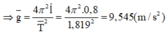
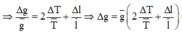
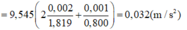
Do đó: g = 9,545 ± 0,032 m/s => Chọn A

\(T=2\pi\sqrt{\frac{\Delta l_0}{9}}=0,4s\)
\(\Rightarrow\Delta l_0=4=\frac{A\sqrt{2}}{2}\)
Thời gian lò xo không giãn là \(t=2t-\frac{A\sqrt{2}}{2}\Rightarrow-A=\frac{T}{4}=0,10\left(s\right)\)
Vậy D đúng
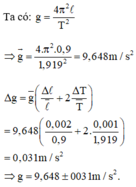
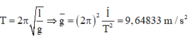
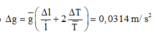
Đáp án B