
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

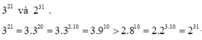

a) 3\(^{21}\) = (3\(^7\))\(^3\) = 2187\(^3\)
2\(^{31}\) < 2\(^{33}\) = (2\(^{11}\))\(3\) = 2048\(^3\)
\(\Rightarrow\) 3\(^{21}\) > 2\(^{33}\)
\(\Rightarrow3^{21}>2^{31}\)

Ta có :
321 = 3.320 = 3.910
231 = 2.230 = 2.810
Vì 3.910 > 2.810 nên 321 > 231
Ta có:231=(23)10.2=810.2
321=(32)10.3=910.3
Vì \(\hept{\begin{cases}9^{10}>8^{10}\\3>2\end{cases}}\) nên 910.3>810.2 hay 321>231

3^39<3^40=9^20
11^21>11^20
Vì 9^20<11^20
=>3^39<11^21
Nhớ k mik nhé, cảm ơn bạn nhìu!

\(3^{21}=3^{20}.3=9^{10}.3>8^{10}.2=2^{31}\)
Do đó \(3^{21}>2^{31}\)
321 = 920
231 = 430
ta có (43)10 = 6410
920 = (92)10 = 8110
vì 81 > 64 => 321 > 231

\(Ta\)\(có\)\(5^{36}=\left(5^3\right)^{12}=125^{12}\)
\(11^{24}=\left(11^2\right)^{12}=121^{12}\)
\(Mà\)\(125^{12}>121^{12}\)
\(=>5^{36}>11^{24}\)
Ta có:
\(5^{36}=\left(5^3\right)^{12}=125^{12}\)
\(11^{24}=\left(11^2\right)^{12}=121^{12}\)
\(Do125>121\)
\(\Rightarrow125^{12}>121^{12}\)
\(\Rightarrow5^{36}>11^{24}\)

2^31=2*2^30=2*8^10
3^21=3*3^20=3*9^10
vì 2*8^10<3*9^10
vậy 2^31<3^21

\(3^{21};2^{31}\)
2^31= (2^3)^10 x 2= 8^10 x 2
3^21= (3^2)^10 x 3= 9^10 x 3
=> 3^21>2^31

\(\left(\frac{1}{3}\right)^{202}=\left[\left(\frac{1}{3}\right)^2\right]^{101}=\left(\frac{1}{9}\right)^{101}=\frac{1}{9^{101}}\)
\(\left(\frac{1}{2}\right)^{303}=\left[\left(\frac{1}{2}\right)^3\right]^{101}=\left(\frac{1}{8}\right)^{101}=\frac{1}{8^{101}}\)
Ta có: \(9>8\Rightarrow9^{101}>8^{101}\Rightarrow\frac{1}{9^{101}}< \frac{1}{8^{101}}\)
\(\Rightarrow\left(\frac{1}{2}\right)^{303}>\left(\frac{1}{3}\right)^{202}\)