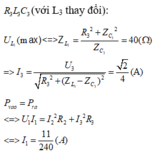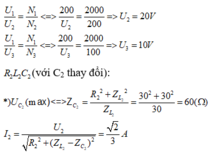Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Dựa vào giản đồ xét tam giác vuông OAB có
\(\sin60=\frac{Uc}{U_{ }AB}\Rightarrow U_C=100.\sin60=50\sqrt{3}V\Rightarrow Z_C=\frac{U_C}{I}=\frac{50\sqrt{3}}{0.5}=100\sqrt{3}\Omega\)
=> \(C=\frac{1}{Z_C.\omega}\)
\(\cos60=\frac{U_R}{U_{AB}}\Rightarrow U_R=50\Omega\Rightarrow R=\frac{U_R}{I}=100\Omega\)
2. Công suất trên mạch có biểu thức
\(P=I^2R=\frac{U^2}{R^2+\left(Z_L-Z_C\right)^2}.R\\=\frac{U^2}{R^{ }+\frac{\left(Z_L-Z_C\right)^2}{R}}\)
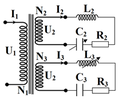
L thay đổi để P max <=> Mẫu Min => áp dụng bất đẳng thức cô-si cho hai số không âm=> \(R=\left|Z_L-Z_C\right|\)
=> \(R=100-40=60\Omega\)
=>

\(U_{RC}=const=U\) khi \(Z_{L1}=2Z_C=R\)
Mặt khác L thay đổi để : \(U_{Lmax}:U_{Lmax}=\frac{U\sqrt{R^2+Z^2_C}}{R}=\frac{U\sqrt{2^2+1}}{2}=\frac{U\sqrt{5}}{2}\)
\(\Rightarrow chọn.D\)
+,có C=C1=>U_R=\frac{U.R}{\sqrt{R^2+(Zl-ZC1)^2}}
+,U R ko đổi =>Zl=ZC1
+,có c=C1/2=>ZC=2ZC1
=>U(AN)=U(RL)=\frac{U\sqrt{r^2+Z^2l}}{\sqrt{R^2+(Zl-2Z^2C1)}}=u=200V

\(\leftrightarrow\frac{u^2_R}{\left(\frac{8}{5}\right)^2}+\frac{u^2_L}{\left(\frac{5}{2}\right)^2}=1\)
Điều kiện :
\(\begin{cases}u_R\le\frac{8}{5}\left(V\right)\\u_L\le\frac{5}{2}\left(V\right)\end{cases}\)
\(\Rightarrow U_{\text{oR}}=\frac{8}{5}\left(V\right);U_{0L}=\frac{5}{2}\left(V\right)\)
\(\Rightarrow\frac{R}{\omega L}=\frac{8}{5}.\frac{2}{5}=\frac{16}{25}\leftrightarrow L=\frac{25R}{16L}=\frac{1}{2\pi}\left(H\right)\)
Đáp án C

Hướng dẫn:
\(U_{AB}=U_C=2\) (1)
\(U_{BC}^2=U_r^2+U_L^2=3\) (2)
\(U_{AC}^2=U_r^2+(U_L-U_C)^2=1\) (3)
Giải hệ 3 pt trên sẽ tìm đc \(U_r\) và \(U_L\)
Chia cho \(I\) sẽ tìm được \(r\) và \(Z_L\)

Giá trị tức thời \(u_m=u_{d1}+u_{d2}\)
Mà theo giả thiết giá trị hiệu dụng \(U_m=U_{d1}+U_{d2}\)
Suy ra ud1 cùng pha với ud2
\(\Rightarrow\tan\varphi_1=\tan\varphi_2\)
\(\Rightarrow\frac{Z_{L1}}{R_1}=\frac{Z_{L2}}{R_2}\)
\(\Rightarrow L_1R_2=L_2R_1\)
Chọn D

Mình giải thích rõ hơn công thức của bạn Nguyễn Trung Thành
iOUUUUULRCRC→→→→→→abc
Nhận xét:
+ Khi L thay đổi thì góc b và c không đổi (do R và ZC không đổi).
+ Khi L = L0 để UL max thì a0 + b = 900.
Áp dụng định lí hàm số sin trong tam giác OULUC:
\( \frac{U_L}{\sin(a+b)}=\frac{U}{\sin c}=const\)
\(\Rightarrow\frac{U_L}{\sin(a_1+b)}=\frac{U_L}{\sin(a_2+b)}\Rightarrow \sin(a_1+b)=\sin(a_2+b)\Rightarrow a_1+b=\pi-(a_2+b)\)
\(\Rightarrow a_1+a_2=\pi-2b\) Mà \(a_0+b=\frac{\pi}{2}\Rightarrow 2a_0=\pi-2b\)
\(\Rightarrow a_1+a_2=2a_0\)
Hay: \(\varphi_0=\frac{\varphi_1+\varphi_2}{2}\)
Áp dụng công thức: \(\varphi_0=\frac{\varphi_1+\varphi_2 }{2}\Rightarrow\varphi_0=\frac{0,56+0,98 }{2}=0,77\)
\(\Rightarrow \cos\varphi_0=\cos0,77=0,72\)
Đáp án B.