Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(u_M= 5\cos(4\pi t - 2 \pi \frac{d}{\lambda}) = 5\cos(4\pi t - 2 \pi \frac{50}{20})=5\cos(4\pi t - 5 \pi) cm.\)

Hai điểm có cùng biên độ 2 mm đối xứng nhau qua nút gần nhất và hai điểm có biên độ 3 mm nằm đồi xứng nhau qua bụng gần nhất. Áp dụng công thức tình biên độ điểm, ta có hệ phương trình:
Gọi biên độ sóng tại bụng là 2a.
Ta có : \(\frac{1}{a^2}=\frac{9}{4a^2}=1\rightarrow a=\frac{2}{\sqrt{13}}\)
Xét: \(2a\sin\frac{2\pi x}{\lambda}=2\rightarrow2\lambda=54cm\Rightarrow\lambda=27cm\)
Vậy chọn đáp án A.

lúc t=0 đầu O bắt đầu dao động đi lên thì tại điểm M vẫn chưa dao động
Vậy muốn M đến vị trí cao nhất thì sóng phải chuyền từ O --> M sau đó từ M --> vị trí cao nhất
Vậy \(t=\frac{OM}{v}+\frac{T}{4}=\frac{1,4}{2}+0,5=1,2s\)
Chọn D

Đây em nhé Câu hỏi của Nguyễn Thị Trúc Đào - Vật lý lớp 12 | Học trực tuyến

Đáp án: C
HD Giải: Thời gian sóng truyền từ O đến M là t = 1,4/2 = 0,7s. Thời gian để M đi từ VTCB lên đến điểm N thấp hơn VTCB 2 cm là
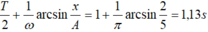

Thời gian cần tìm là 0,7 + 1,13 = 1,83 s

Hướng dẫn: Chọn đáp án B
Khi t = 0 điểm O mới bắt đầu dao động đi lên thì sau thời gian OM/v sóng mới truyền đến M và M bắt đầu dao động đi lên, sau đó một khoảng thời gian T/4 điểm M mới đến vị trí cao nhất và tiếp theo khoảng thời gian T/2 nữa thì nó xuống đến vị trí thấp nhất. Thời điểm đầu tiên để M đến điểm thấp nhất:


Trong 1 chu kì , thời gian li độ của B có độ lớn hơn biên độ của C là T/3
=> Thời gian ngắn nhất để li độ điểm B đi từ biên độ đến vị trí li độ bằng điên độ tại C là T/12
\(\Rightarrow\Delta\varphi=\frac{2\pi d}{\lambda}=\frac{\pi}{6}\Rightarrow d=\frac{\lambda}{12}\)

Từ đề bài ta suy ra M và N là vị trí có li độ \(\frac{\left|A\right|\sqrt{3}}{2}\)
\(\rightarrow\frac{T}{6}=0,05s\rightarrow T=0,3s\)
Ta có :
\(\upsilon=\frac{\upsilon_{max}}{2}\rightarrow\upsilon_{max}=40\pi\left(cm\text{ / s }\right)\rightarrow A\text{ω }=A.\frac{2\pi}{T}=40\pi\)
→ A = 6cm
Đáp án: D
HD Giải: Thời gian sóng truyền từ O đến M là t = 1,4/2 = 0,7s. Thời gian để M đi từ VTCB lên đến điểm cao nhất là T/4 = 0,5 s. Thời gian cần tìm là 0,7 + 0,5 = 1,2s