Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có :
\(K=\frac{2\sqrt{x}+3}{\sqrt{x}-5}=\frac{2\sqrt{x}-10}{\sqrt{x}-5}+\frac{13}{\sqrt{x}-5}=2+\frac{13}{\sqrt{x}-5}\)là số nguyên dương
<=> 13 chia hết cho \(\sqrt{x}-5\)
<=> \(\sqrt{x}-5\inƯ\left(13\right)=\left\{-13;-1;1;13\right\}\)
<=> \(\sqrt{x}\in\left\{-12;4;6;18\right\}\)
<=> \(x\in\left\{16;36;324\right\}\) (vì \(\sqrt{x}\ge0\))
Do x nguyên và x có GTLN nên x = 324

Đáp án A
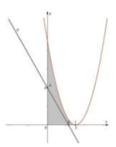
Phương trình hoành độ giao điểm của đồ thị hàm số y = x 2 − 6 x + 9 và trục hoành là:
x 2 − 6 x + 9 = 0 ⇔ x = 0 .
Diện tích hình phẳng (H) giới hạn bởi đồ thị hàm số y = x 2 − 6 x + 9 và 2 đường thẳng x= 0; y = 0 là:
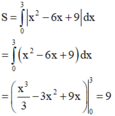
Phương trình đường thẳng (d) có hệ số góc k và cắt trục tung tại điểm A(0;4) là: y = kx +4
Gọi B là giao điểm của (d) và trục hoành ⇒ B − 4 k ; 0 .
Để (d) chia (H) thành 2 phần có diện tích bằng nhau thì:
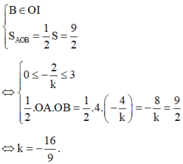 .
.

Đáp án A
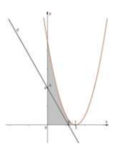
Phương trình hoành độ giao điểm của đồ thị hàm số y = x 2 − 6 x + 9 và trục hoành là:
x 2 − 6 x + 9 = 0 ⇔ x = 0 .
Diện tích hình phẳng (H) giới hạn bởi đồ thị hàm số y = x 2 − 6 x + 9 và 2 đường thẳng x= 0; y = 0 là:
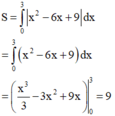
Phương trình đường thẳng (d) có hệ số góc k và cắt trục tung tại điểm A(0;4) là: y = kx +4
Gọi B là giao điểm của (d) và trục hoành ⇒ B − 4 k ; 0 .
Để (d) chia (H) thành 2 phần có diện tích bằng nhau thì:
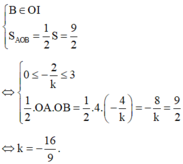

Đáp án A
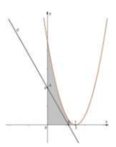
Phương trình hoành độ giao điểm của đồ thị hàm số y = x 2 − 6 x + 9 và trục hoành là:
x 2 − 6 x + 9 = 0 ⇔ x = 0 .
Diện tích hình phẳng (H) giới hạn bởi đồ thị hàm số y = x 2 − 6 x + 9 và 2 đường thẳng x= 0; y = 0 là:
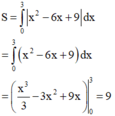
Phương trình đường thẳng (d) có hệ số góc k và cắt trục tung tại điểm A(0;4) là: y = kx +4
Gọi B là giao điểm của (d) và trục hoành ⇒ B − 4 k ; 0 .
Để (d) chia (H) thành 2 phần có diện tích bằng nhau thì:
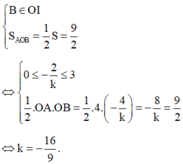

Đáp án D
Phương trình hoành độ giao điểm của (C)và trục Ox là ln x = 0 ⇔ x = 1
Diện tích hình phẳng (H) là S = π . ∫ 1 k lnx d x = π . ∫ 1 k lnx d x . Đặt u = ln x d v = d x ⇔ d u = d x x v = x .
⇒ ∫ 1 1 ln x d x = x . ln x 1 k - ∫ 1 k d x = x . ln x - x 1 k = k . ln k - k + 1 = 1 ⇔ ln k = 1 ⇔ k = e .

Đáp án D
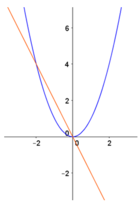
Hoành độ giao điểm của đồ thị hàm số y = a x 2 và đồ thị hàm số y = - b x là nghiệm của phương trình
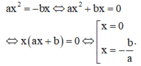
Thể tích khối tròn xoay được tạo thành
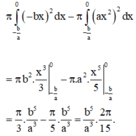
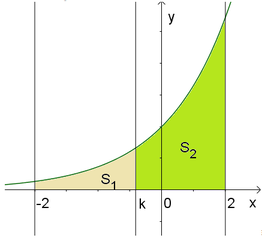
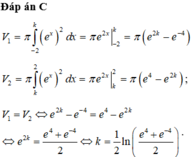

( E ) : x 2 16 + y 2 9 = 1 ⇒ y = ± 3 4 16 - x 2
Đường thằng x = k chia elip thành hai phần (H) và (K) khi đó
V H = π ∫ - 4 k 3 14 16 - x 2 dx = 1 4 π 48 x - x 3 - 4 k = 1 4 π 48 k - k 3 + 128
V H V K = 48 k - k 3 + 128 128 - 48 k + k 3 = 5 27 ⇒ 48 k - k 3 + 128 256 = 5 32 ⇒ k 3 - 48 k - 88 = 0
với k nguyên âm k = -2
Đáp án cần chọn là C