Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài giải:
a) 3x2 – 2x = x2 + 3 ⇔ 2x2 – 2x - 3 = 0.
b’ = -1, ∆’ = (-1)2 – 2 . (-3) = 7
x1 = ≈ 1, 82; x2 =
≈ -0,82
b) (2x - √2)2 – 1 = (x + 1)(x – 1) ⇔ 3x2 - 4√2 . x + 2 = 0 . b’ = -2√2
∆’ = (-2√2)2 – 3 . 2 = 2
x1 = = √2 ≈ 1,41; x2 =
=
≈ 0,47.
c) 3x2 + 3 = 2(x + 1) ⇔ 3x2 – 2x + 1 = 0.
b’ = -1; ∆’ = (-1)2 – 3 . 1 = -2 < 0
Phương trình vô nghiệm.
d) 0,5x(x + 1) = (x – 1)2 ⇔ 0,5x2 – 2,5x + 1 = 0
⇔ x2 – 5x + 2 = 0, b’ = -2,5; ∆’ = (-2,5)2 – 1 . 2 = 4,25
x1 = 2,5 + √4,25 ≈ 4,56, x2 = 2,5 - √4,25 ≈ 0,44
(Rõ ràng trong trường hợp này dung công thức nghiệm thu gọn cũng không đơn giản hơn)
a) 3x2 – 2x = x2 + 3 ⇔ 2x2 – 2x - 3 = 0.
b’ = -1, ∆’ = (-1)2 – 2 . (-3) = 7
x1 = ≈ 1, 82; x2 =
≈ -0,82
b) (2x - √2)2 – 1 = (x + 1)(x – 1) ⇔ 3x2 - 4√2 . x + 2 = 0 . b’ = -2√2
∆’ = (-2√2)2 – 3 . 2 = 2
x1 = = √2 ≈ 1,41; x2 =
=
≈ 0,47.
c) 3x2 + 3 = 2(x + 1) ⇔ 3x2 – 2x + 1 = 0.
b’ = -1; ∆’ = (-1)2 – 3 . 1 = -2 < 0
Phương trình vô nghiệm.
d) 0,5x(x + 1) = (x – 1)2 ⇔ 0,5x2 – 2,5x + 1 = 0
⇔ x2 – 5x + 2 = 0, b’ = -2,5; ∆’ = (-2,5)2 – 1 . 2 = 4,25
x1 = 2,5 + √4,25 ≈ 4,56, x2 = 2,5 - √4,25 ≈ 0,44

0,5x(x + 1) = (x – 1)2
⇔ 0,5x2 + 0,5x = x2 – 2x + 1
⇔ x2 – 2x + 1 – 0,5x2 – 0,5x = 0
⇔ 0,5x2 – 2,5x + 1 = 0
⇔ x2 – 5x + 2 = 0
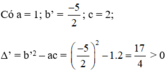
Phương trình có hai nghiệm phân biệt:
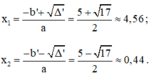

3x2 + 3 = 2(x + 1)
⇔ 3x2 + 3 = 2x + 2
⇔ 3x2 + 3 – 2x – 2 = 0
⇔ 3x2 – 2x + 1 = 0
Phương trình có a = 3; b’ = -1; c = 1; Δ’ = b’2 – ac = (-1)2 – 3.1 = -2 < 0
Vậy phương trình vô nghiệm.

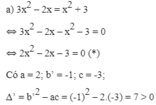
Phương trình (*) có hai nghiệm phân biệt:
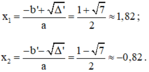

Có: a = 3; b’ = -2√2; c = 2;
Δ ’ = b ’ 2 – a c = ( - 2 √ 2 ) 2 – 3 . 2 = 2 > 0
Vì Δ’ > 0 nên phương trình có hai nghiệm phân biệt là:
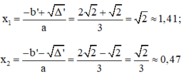
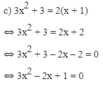
Phương trình có a = 3; b’ = -1; c = 1;
Δ ’ = b ’ 2 – a c = ( - 1 ) 2 – 3 . 1 = - 2 < 0
Vậy phương trình vô nghiệm.
d)
0 , 5 x ( x + 1 ) = ( x – 1 ) 2 ⇔ 0 , 5 x 2 + 0 , 5 x = x 2 – 2 x + 1 ⇔ x 2 – 2 x + 1 – 0 , 5 x 2 – 0 , 5 x = 0 ⇔ 0 , 5 x 2 – 2 , 5 x + 1 = 0 ⇔ x 2 – 5 x + 2 = 0
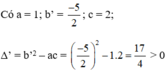
Phương trình có hai nghiệm phân biệt:
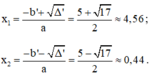

3x2 – 2x = x2 + 3
⇔ 3x2 – 2x – x2 – 3 = 0
⇔ 2x2 – 2x – 3 = 0 (*)
Có a = 2; b’ = -1; c = -3; Δ’ = b’2 – ac = (-1)2 – 2.(-3) = 7 > 0
Phương trình (*) có hai nghiệm phân biệt:
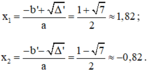

a)

b) \(\dfrac{1}{2}x^2-2x+1=0\Leftrightarrow x^2-4x+2=0\)
\(\Leftrightarrow x_1=2-\sqrt{2}\approx0,59\) \(x_2=2+\sqrt{2}\approx3,41\)

a) \(x^2=2\Rightarrow x=\sqrt{2}=1,414\)
b) \(x^2=3\Rightarrow x=\sqrt{3}=1,732\)
c) \(x^2=3,5\Rightarrow x=\sqrt{3,5}=1,871\)
d) \(x^2=4,12\Rightarrow x=\sqrt{4,12}=2,030\)

a: =>(4x-1)2=0
=>4x-1=0
hay x=1/4=0,25
b: \(6x^2-10x-1=0\)
\(\Delta=\left(-10\right)^2-4\cdot6\cdot\left(-1\right)=100+24=124>0\)
Do đó; Phương trình có hai nghiệm phân biệt là:
\(\left\{{}\begin{matrix}x_1=\dfrac{10-2\sqrt{31}}{12}\simeq-0,09\\x_2=\dfrac{10+2\sqrt{31}}{12}\simeq1,76\end{matrix}\right.\)
c: \(5x^2+24x+9=0\)
\(\Delta=24^2-4\cdot5\cdot9=396>0\)
Do đó: Phương trình có hai nghiệm phân biệt là:
\(\left\{{}\begin{matrix}x_1=\dfrac{-24-2\sqrt{99}}{10}\simeq-4,39\\x_2=\dfrac{-24+2\sqrt{99}}{10}\simeq-0,41\end{matrix}\right.\)
d: \(16x^2-10x+1=0\)
\(\Delta=\left(-10\right)^2-4\cdot16\cdot1=100-64=36>0\)
Do đó: Phương trình có hai nghiệm phân biệt là
\(\left\{{}\begin{matrix}x_1=\dfrac{10-6}{64}=\dfrac{4}{64}=\dfrac{1}{16}\\x_2=\dfrac{10+6}{64}=\dfrac{1}{4}\end{matrix}\right.\)
(2x - √2)2 – 1 = (x + 1)(x – 1);
⇔ 4x2 – 2.2x.√2 + 2 – 1 = x2 – 1
⇔ 4x2 – 2.2√2.x + 2 – 1 – x2 + 1 = 0
⇔ 3x2 – 2.2√2.x + 2 = 0
Có: a = 3; b’ = -2√2; c = 2; Δ’ = b’2 – ac = (-2√2)2 – 3.2 = 2 > 0
Vì Δ’ > 0 nên phương trình có hai nghiệm phân biệt là: