
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

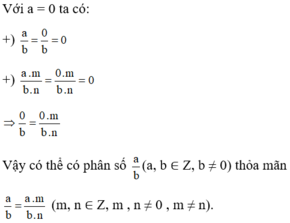

không thể, vì để có phân số mới bằng phân số a/b thì m=n và n khác 0

có phân số a/b (a;b thuộc Z, b khác 0) và a/b = am/bn khi a = 0
VD :
0/b = 0.m/bn
\(\frac{a}{b}=\frac{a}{b}.\frac{m}{n}\Leftrightarrow\frac{a}{b}\left(1-\frac{m}{n}\right)=0\Leftrightarrow\orbr{\begin{cases}\frac{a}{b}=0\\\frac{m}{n}=1\end{cases}}\)
Do \(m\ne n\Rightarrow\frac{m}{n}\ne1\Rightarrow\frac{a}{b}=0\Rightarrow a=0\)
Vậy a=0, b là số nguyên khác 0

Không. Vì không có phân số nào mà cả tử số và mẫu số nhân với hai số khác nhau lại bằng phân số đã cho cả (hay do m khác n)

a) Ta có :
\(A=\frac{n}{n+1}=1-\frac{1}{n+1}\in Z\)
⇔ n + 1 ϵ Ư(1) = { 1 ; - 1 }
⇔ n ϵ { 0 ; - 2 }
b) Lại có :
\(B=\frac{n}{n-1}=1+\frac{1}{n-1}\in Z\)
⇔ n - 1 ϵ Ư(1) = { 1 ; - 1 }
⇔ n ϵ { 2 ; 0 }

Lời giải:
a. Ta thấy $n^2+5\geq 5> 0$ với mọi $n\in\mathbb{Z}$
$\Rightarrow n^2+5\neq 0$ với mọi $n\in\mathbb{Z}$
$\Rightarrow$ phân số $M$ luôn tồn tại.
b.
Với $n=0$ thì $M=\frac{0-3}{0^2+5}=\frac{-3}{5}$
Với $n=2$ thì $M=\frac{2-3}{2^2+5}=\frac{-1}{9}$
Với $n=-5$ thì $M=\frac{-5-3}{(-5)^2+5}=\frac{-4}{15}$

1.Cho A=\(\dfrac{n+1}{n-2}\)
a)Tìm n ∈ Z để A là phân số
Để A là phân số thì n+1;n-2 ∈ Z ; n-2 khác 0
<=> n ∈ Z; n >2
Vậy A là phân số <=> n ∈ Z; n>2
b)Tìm n∈Z để A∈Z
A ∈ Z <=> n+1 chia hết cho n-2
<=>n-2+3 chia hết cho n-2
<=>3 chia hết cho n-2 ( vì n-2 chia hết cho n-2)
<=>n-2 ∈ Ư(3)={1;-1;3;-3}
<=>n ∈ {3;1;5;-1}
Vậy để A ∈ Z thì n ∈ {3;1;5;-1}
c)Tìm N∈Z để A lớn nhất
2.Cho B=\(\dfrac{3n+2}{4n+3}\)
Chứng minh B tối giản
1c) Tìm n∈Z để A lớn nhất:
Ta có A=\(\dfrac{n+1}{n-2}\)=\(\dfrac{n-2+3}{n-2}\)=\(\dfrac{n-2}{n-2}\)+\(\dfrac{3}{n-2}\)=1+\(\dfrac{3}{n-2}\)
=> A lớn nhất <=> \(\dfrac{3}{n-2}\) lớn nhất
<=>n-2 nhỏ nhất; n-2>0; n-2∈Z
<=>n-2=1
<=>n=3
Vậy A lớn nhất <=> n-3

\(a,\text{ Để A }\in\text{ Z }\Leftrightarrow\text{ }\left(n+1\right)\inƯ\left(2\right)\)
\(\text{Mà }Ư\left(2\right)=\left\{\pm1;\pm2\right\}\)
\(\text{Do đó:}\) \(n+1=1\Leftrightarrow n=0\)
\(\text{hoặc }n+1=-1\Leftrightarrow n=-2\)
\(\text{hoặc }n+1=2\Leftrightarrow n=1\)
\(\text{hoặc }n+1=-2\Leftrightarrow n=-3\)
\(\text{Vậy: A }\in Z\Leftrightarrow n=\left\{0;-2;1;-3\right\}.\)
\(\text{a) Để B}\in Z\Leftrightarrow n-2\inƯ\left(3\right)\)
\(\text{Mà }Ư\left(3\right)=\left\{\pm1;\pm3\right\}\)
\(\text{Do đó: }n-2=1\Leftrightarrow n=3\)
\(\text{hoặc }n-2=-1\Leftrightarrow n=1\)
\(\text{hoặc }n-2=3\Leftrightarrow n=5\)
\(\text{hoặc }n-2=-3\Leftrightarrow n=-1\)
\(\text{Vậy: B}\in Z\Leftrightarrow n=\left\{3;1;5;-1\right\}.\)