
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

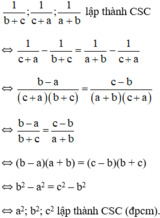

TenAnh1 TenAnh1 A = (-4.36, -6.06) A = (-4.36, -6.06) A = (-4.36, -6.06) B = (11, -6.06) B = (11, -6.06) B = (11, -6.06)

Theo đầu bài ta có : \(\cot\frac{A}{2}+\cot\frac{C}{2}=2\cot\frac{B}{2}\Leftrightarrow\frac{\sin\frac{A+C}{2}}{\sin\frac{A}{2}\sin\frac{C}{2}}=2\frac{\cos\frac{B}{2}}{\sin\frac{B}{2}}=2\frac{\sin\frac{A+C}{2}}{\cos\frac{A+C}{2}}\)
\(\Leftrightarrow\sin\left(\frac{A+C}{2}\right)\cos\left(\frac{A+C}{2}\right)=2\sin\frac{A}{2}\sin\frac{C}{2}\sin\frac{A+C}{2}=\left(\cos\frac{A-C}{2}-\cos\frac{A+C}{2}\right)\sin\frac{A+C}{2}\)
\(\Leftrightarrow2\sin\frac{A+C}{2}\cos\frac{A+C}{2}=\cos\frac{A-C}{2}\sin\frac{A+C}{2}\)
\(\Leftrightarrow2\sin\left(A+C\right)=\frac{1}{2}\left(\sin A+\sin C\right)\)
\(\Leftrightarrow\sin A+\sin C=2\sin B\Rightarrow a+c=2b\)
Chứng tỏ 3 cạnh của tam giác lập thành cấp số cộng

Theo giả thiết ta có : \(\cot A+\cot C=2\cot B\)
\(\Leftrightarrow\frac{\sin\left(A+C\right)}{\sin A\sin C}=\frac{2\cos B}{\sin B}\)
\(\Leftrightarrow\sin^2B=2\sin B\sin C\cos B=\left[\cos\left(A-C\right)-\cos\left(A+C\right)\right]\cos B\)
\(\Leftrightarrow\sin^2B=\cos\left(A-C\right)\cos B-\cos\left(A+C\right)\cos B=-\cos\left(A-C\right)\cos\left(A+C\right)+\cos^2B\)
\(\Leftrightarrow\sin^2B=-\frac{1}{2}\left(\cos2A+\cos2C\right)+1-\sin^2B=-\frac{1}{2}\left(1-2\sin^2A+1-2\sin^2C\right)+1-\sin^2B\)
\(\Rightarrow2\sin^2B=\sin^2A+\sin^2C\Leftrightarrow2b^2=a^2+c^2\)
Vậy chứng tỏ \(a^2,b^2,c^2\) theo thứ tự đó cũng lập thành một cấp số cộng

\(a,b,c\)theo thứ tự lập thành cấp số cộng nên \(a-b=b-c\).
\(d\)là công sai của cấp số cộng.
Nếu \(d=0\)dễ dàng thấy đẳng thức cần chứng minh là đúng.
Nếu \(d\ne0\):
\(\frac{1}{\sqrt{a}+\sqrt{b}}+\frac{1}{\sqrt{b}+\sqrt{c}}=\frac{\sqrt{a}-\sqrt{b}}{a-b}+\frac{\sqrt{b}-\sqrt{c}}{b-c}=\frac{\sqrt{a}-\sqrt{c}}{a-b}\)
\(=\frac{a-c}{\left(a-b\right)\left(\sqrt{a}+\sqrt{c}\right)}=\frac{2}{\sqrt{a}+\sqrt{c}}\)
<br class="Apple-interchange-newline"><div></div>a,b,ctheo thứ tự lập thành cấp số cộng nên a−b=b−c.
dlà công sai của cấp số cộng.
Nếu d=0dễ dàng thấy đẳng thức cần chứng minh là đúng.
Nếu d≠0:
1√a+√b +1√b+√c =√a−√ba−b +√b−√cb−c =√a−√ca−b
=a−c(a−b)(√a+√c) =2√a+√c

Nếu 3 cạnh a, b, c lập thành cấp số cộng thì ta có a + c = 2b
\(\Leftrightarrow\sin A+\sin C=2\sin B\Leftrightarrow2\sin\frac{A+C}{2}\cos\frac{A-C}{2}=4\sin\frac{B}{2}\cos\frac{B}{2}\left(1\right)\)
Vì \(A+C=180^0-B\Rightarrow\frac{A+C}{2}=90^0-\frac{B}{2}\)
<=> \(\sin\frac{A+C}{2}=\sin\left(90^0-\frac{B}{2}\right)=\cos\frac{B}{2}\) hoặc \(\cos\frac{A+C}{2}=\cos\left(90^0-\frac{B}{2}\right)=\sin\frac{B}{2}\) (*)
Do đó (1) trở thành :
\(\Leftrightarrow\sin\frac{A+C}{2}\cos\frac{A-C}{2}=2\sin\frac{A+C}{2}\cos\frac{A+C}{2}\)
\(\Leftrightarrow\cos\frac{A-C}{2}=2\sin\frac{B}{2}\)
\(\Leftrightarrow\cos\frac{A-C}{2}=2\cos\frac{A+C}{2}\)
\(\Leftrightarrow\cos\frac{A}{2}\cos\frac{C}{2}+\sin\frac{A}{2}\sin\frac{C}{2}=2\cos\frac{A}{2}\cos\frac{C}{2}-2\sin\frac{A}{2}\sin\frac{C}{2}\)
\(\Leftrightarrow\cos\frac{A}{2}\cos\frac{C}{2}=3\sin\frac{A}{2}\sin\frac{C}{2}\)
\(\Leftrightarrow\cot\frac{A}{2}\cot\frac{C}{2}=3\) => Điều phải chứng minh

Lời giải:
Nếu $a,b,c$ lập thành csc thì $b=a+m, c=a+2m$ với $m$ là công sai.
Khi đó:
$3(a^2+b^2+c^2)-6(a-b)^2=3[a^2+(a+m)^2+(a+2m)^2]-6(a-a-m)^2$
$=3(a^2+a^2+m^2+2am+a^2+4m^2+4am)-6m^2$
$=3(3a^2+5m^2+6am)=9a^2+15m^2+18am-6m^2$
$=9a^2+9m^2+18am$
$=9(a^2+m^2+2am)=9(a+m)^2=(3a+3m)^2$
$=(a+a+m+a+2m)^2=(a+b+c)^2$ (đpcm).

Ba số \(\frac{2}{{b - a}},\frac{1}{b},\frac{2}{{b - c}}\) theo thứ tự lập thành cấp số cộng nên ta có:
\(\begin{array}{l}\frac{2}{{b - a}} + \frac{2}{{b - c}} = 2.\frac{1}{b} \Leftrightarrow \frac{1}{{b - a}} + \frac{1}{{b - c}} = \frac{1}{b} \Leftrightarrow \frac{{\left( {b - c} \right) + \left( {b - a} \right)}}{{\left( {b - a} \right)\left( {b - c} \right)}} = \frac{1}{b}\\ \Leftrightarrow \frac{{b - c + b - {\rm{a}}}}{{{b^2} - ab - bc + ac}} = \frac{1}{b} \Leftrightarrow \frac{{2b - c - {\rm{a}}}}{{{b^2} - ab - bc + ac}} = \frac{1}{b} \Leftrightarrow b\left( {2b - c - {\rm{a}}} \right) = {b^2} - ab - bc + ac\\ \Leftrightarrow 2{b^2} - bc - {\rm{ab}} = {b^2} - ab - bc + ac \Leftrightarrow {b^2} = {\rm{a}}c\end{array}\).
Vậy ba số \(a,b,c\) theo thứ tự lập thành cấp số nhân.

Theo giả thiết :
\(\Leftrightarrow\log_xa+\log_zc=2\log_yb\)
\(\Leftrightarrow\frac{1}{\log_ax}+\frac{1}{\log_cz}=\frac{2}{\log_by}\)
\(\Rightarrow\frac{1}{\log y_b}=\frac{2\log_ax.\log_cz}{\log_ax+\log_cz}\)
\(\Rightarrow\) Điều phải chứng minh