Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi R là bán kính của đường tròn (C)
(C) và C1 tiếp xúc ngoài với nhau, cho ta:
MF1 = R1+ R (1)
(C) và C2 tiếp xúc ngoài với nhau, cho ta:
MF2 = R2 – R (2)
Từ (1) VÀ (2) ta được
MF1 + MF2 = R1+ R2= R không đổi

Điểm M có tổng các khoảng cách MF1 + MF2 đến hai điểm cố định F1 và F2 bằng một độ dài không đổi R1+ R2
Vậy tập hợp điểm M là đường elip, có các tiêu điểm F1 và F2 và có tiêu cự
F1 .F2 = R1+ R2


\(a=2;b=1\Rightarrow c=\sqrt{3}\)
\(\Rightarrow F_1F_2=2c=2\sqrt{3}\)
\(MF_1\perp MF_2\Rightarrow\Delta MF_1F_2\) vuông tại M
\(\Rightarrow MF_1^2+MF_2^2=F_1F_2^2=12\) (Pitago)
Ta có: \(\left\{{}\begin{matrix}MF_1^2+MF_2^2=12\\MF_1+MF_2=2a=4\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}MF_1^2+MF_2^2=12\\\left(MF_1+MF_2\right)^2=16\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}MF_1^2+MF_2^2=12\\MF_1^2+MF_2^2+2MF_1MF_2=16\end{matrix}\right.\)
\(\Rightarrow MF_1.MF_2=2\)
\(\Rightarrow S_{MF_1F_2}=\frac{1}{2}MF_1.MF_2=1\)

mk chỉ cho cách lm ; bn tự lm cho bt nha
câu a : lập bảng sét dấu tìm được \(x\) để \(y>0;y< 0\)
tiếp là đưa nó về dạng bình phương 1 số cộng 1 số \(\left(n^2+m\right)\) rồi tìm \(y_{min}\)
câu b : giao điểm của \(\left(P\right)\) và đường thẳng \(\left(d\right):y=2x+1\)
là nghiệm của hệ phương trình : \(\left\{{}\begin{matrix}y=x^2-2x-1\\y=2x+1\end{matrix}\right.\)

Đề bài thiếu rồi bạn, cần hạn chế hàm \(f\left(x\right)\) vì hàm \(f\left(x\right)\) bất kì thì miền xác định D của nó cũng bất kì.
Nếu hàm \(f\left(x\right)\) có miền xác định ko đối xứng (ví dụ \(y=\sqrt{x}\)) thì không thể tách thành 2 hàm chẵn lẻ vì \(f\left(x\right)=g_1\left(x\right)+g_2\left(x\right)\) thì đương nhiên \(g_1\left(x\right)\) và \(g_2\left(x\right)\) cùng miền xác định với \(f\left(x\right)\). Mà một hàm số có miền xác định không đối xứng thì không thể là hàm chẵn hay hàm lẻ.
Ta có: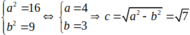
- Tiêu điểm là: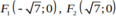
Chọn A